Clicking the Schedule button at the top of the activity worksheet presents the dialog to the left. For purposes of constructing the Gantt chart, time is divided into discrete intervals called time buckets. The interval may be any positive number that gives a Gantt chart with no more than 100 columns. The most convenient intervals are integers. The interval is entered into the Time Bucket field of the dialog. The default Time Horizon is the greater of the due time of the project or the completion time of the schedule on the project worksheet. The latter may be larger if the schedule is late. The Extra Time is the time beyond the time horizon that the completion time might be delayed by the schedule. The sum of the time horizon and the extra time is the maximum time for the Gantt chart. The program limits the total number of intervals in the Gantt chart to 100. The maximum time divided by the time bucket must be less than 100, so the time bucket cannot be too small.

Two methods are provided for dealing with resources. The Limit option specifies a limit for each resource and penalizes any usage above the limit. We try to find schedules that minimize resources used above the limits. The Level option computes the variance of the usage over time. Here we try to find schedules that level the resource usage by minimizing the variance.

Clicking OK constructs the Schedule worksheet on which schedules can be evaluated and optimized. This is particularly useful when a project uses limited resources or involves cash flow. Part of the worksheet constructed for the example is shown below. Formulas link the data in column F through I to cells on the project worksheet. Most of the cells on the schedule worksheet are yellow indicating that their contents are computed with formulas. This is an important distinction, because the formulas are destroyed if the user types values in these cells. Cells with

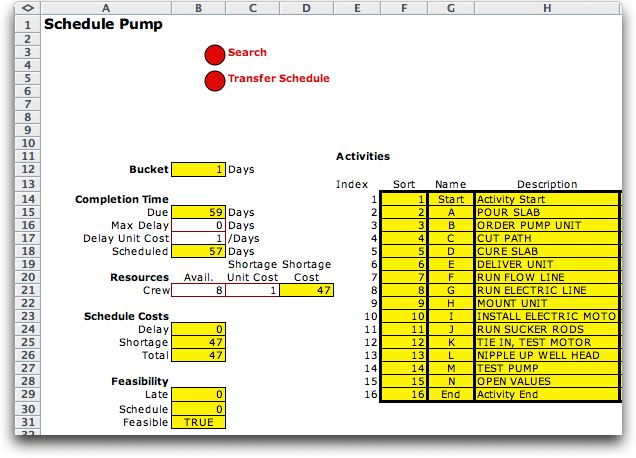
Columns B through D holds data and results for the schedule. Cell B15 holds the due date entered on the project worksheet and B18 holds the completion date for the current schedule. For illustration we have set the crew availability to 8 and the shortage cost of 1 for each crew used in excess of 8. We will discuss other aspects of the solution below. Columns F though H hold data transferred from the definitions on the project worksheet except that on the schedule worksheet the activities are listed in precedence order. For the example, this does not change the order, but that is not true in general.

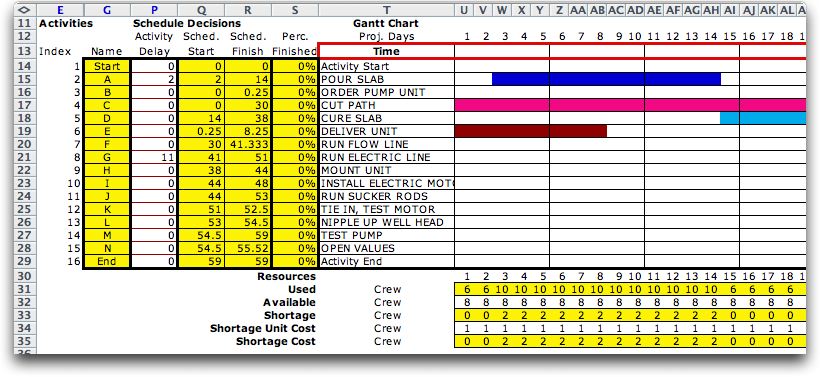
The figure below shows the schedule information on the schedule worksheet. All the columns shown in yellow are governed by formulas. The delays shown in column P may be changed by the user to affect the schedule. Ultimately, column P will be manipulated by algorithms provided by the add-in to search for the optimum schedule.

Times in column J are the mean activity time values. Columns K through N use critical path analysis to compute early and late start times. The resultant slack appears in column O. The slack value is the how much the activity may be delayed without extending the finish date of the project. Column P holds the delay decisions. The initial contents of this column are the delays entered on the project worksheet. We color column P white to indicate that it may be manipulated by hand, but the computer will replace its contents when the Search button is clicked. As the delays change, the slack values will change as well as a number of other cells on this worksheet.

The start and finish times for the activities, in columns Q and R, depend on the delays entered in column P. Column S holds the percentage finished for each activity based on the current time. The current time for this example is 0. Most of the active cells on this worksheet are colored yellow to indicate that they contain Excel formulas. The formulas makes the results dynamic. When data for activity times or resource amounts change, for instance, the results are automatically adjusted. If the number of activities or any of the precedence relations change, this worksheet is no longer valid. The revised project must be solved with the Solve button on the project worksheet. The Schedule worksheet must then be rebuilt using the Schedule button on the project worksheet.

A Gantt chart is shown to the right of the activity data. This is a dynamic chart that changes as the delay entries are manipulated. The colors of the Gantt chart are defined on the project worksheet.The chart stretches across the worksheet for as many intervals as required by the completed project. The current time is 0 for the example and the chart shows the early start schedule. Activity B is very short and is not shown on the chart because of the discrete time bucket of 1. Similarly, times with fractional values are adjusted to integer values for the display. For example the start time of E is 0.25 is rounded down to 1 for the display.

Below the chart, are rows that compute the amount of each resource used in each interval. For the example, the single resource is shown in row 31. The numbers in row 32 are the amounts of the resource that are available. The example uses a limit of 8. These numbers are linked to the the number in cell B21. The numbers can be varied manually to represent the amounts available during the various intervals of the schedule, but the link to cell B21 will be lost. Row 33 holds the amounts of the resource used that exceed the amounts available, or the shortages. The example shows a shortage of 2 for the first 12 periods. Row 34 holds the unit shortage cost that is linked to cell C21. Again the entries in this row may be manually adjusted if the cost varies with time. Row 35 holds the product of rows 33 and 34, the cost of the shortage for each interval.

We focus on the recourse calculations to show more columns. The shortage is 0 for periods 13 through 30 and then goes to 1. The total shortage cost or this solution is 47.

The results for this schedule are shown in columns B through D. The Due time in B15 is transferred from the project worksheet. The Max Delay is entered by the user in B16. This is the time that the project may be delayed beyond the due time. If the schedule on the project worksheet was late when the schedule worksheet was created, the late value is entered here. The entry in cell B17 is the cost per unit time associated with this delay. The Scheduled completion time is 57 (cell B18). Starting in row 21, the cells in column B show the availabilities of each resource. Column C shows the unit cost of exceeding the availabilities. Columns B and C are entered by the user. Column D holds the computed cost of shortages for the current schedule. The evaluation of the schedule starts in row 24. Cell B24 computes the cost due to project delay and cell B25 holds the total resource shortage cost. The Total cost in B26 is the sum of the delay and shortage costs. When we optimize, this is one of the measures that can be included in the objective function.

Feasibility conditions for the schedule start in row 29. The Late entry in cell B29 is the difference between the Scheduled Completion time and the sum of the Due Time and the Maximum Delay. The program does not accept a solution when this value is greater than 0. The Schedule entry in cell B30 is the sum of the times the activities start before their earliest start times. Again, the program does not accept solutions that violate the start times restriction. The entry is cell B31 is True only when both of the preceding amounts are 0. Otherwise it is False. The automatic search process checks this cell as it varies the solution to assure that only feasible solutions are considered.

Search

A specific schedule is obtained by entering nonnegative numbers in the activity delay column. Delays must be multiples of the Time Bucket. A positive delay for some activity will change the schedule limit columns and slack column. Any one delay may be increased by the amount shown in the slack column or decreased by the amount of the current delay. As long as the slack column remains nonnegative, the schedule will be feasible. The figure below shows a schedule with activity A delayed for 2 hours and activity G delayed for 11 hours.

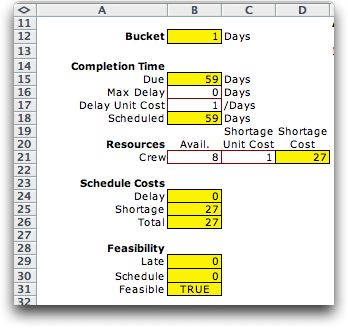Delaying activities automatically changes the Gantt chart and correspondingly the amounts of resources used by the schedule. The results are automatically reflected in the cells of columns B and C. The results for the revised schedule are shown at the left. The total shortage is now 27. This was accomplished by delaying "Pour Slab" by 2 hours and "Run Electric Line" by 11 hours.

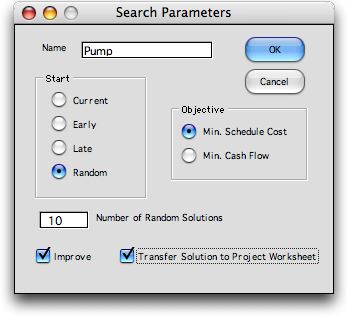
We have programmed a random search process that seeks better solutions. This heuristic is called by clicking the Search button at the top of the worksheet. The dialog below offers the opportunity to either improve the current solution, early start solution, late start solution or to generate random solutions. The number of random solutions is entered in the field at the bottom. Here we have chosen to generate 50 solutions at random and improve each solution with a heuristic procedure.

When the Improve box is checked, the heuristic is applied to the starting solution and each random solution. The Transfer button at the bottom, transfers the solution to the delay column on the project worksheet.

The improvement process considers the activities in order of increasing index, starting at activity 2 (activity 1 is the start activity). If the delay for the activity is not zero, the delay is reduced by 1 time interval. If the cost decreases or remains the same, the delay is reduced further until the cost increases. If the delay is 0 or if reducing the delay results in a cost increase, the delay is increased until the solution cost does not change or increases or until no slack remains. When the next to last activity is complete (the last activity before the end activity), the process has either improved the solution or not. If it has improved the solution, the process repeats, starting again at activity 2. If there is no improvement for a complete cycle through the activities, the improvement process terminates.

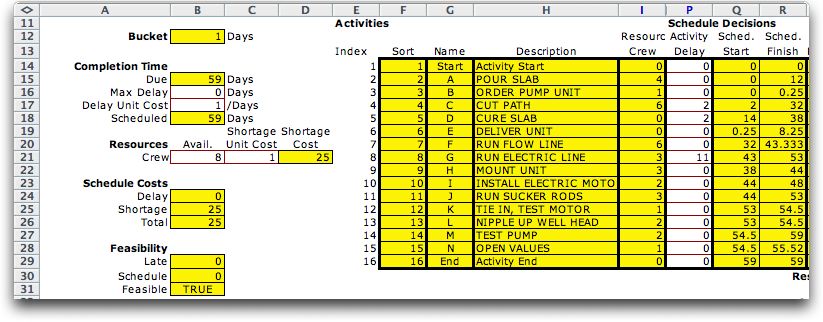
The solution increased the duration of the project to 59 and reduced the shortage cost to 25. The solution with the delays and the resultant schedule are shown below.

A random search selects activities in random order. If the slack for the selected activity is greater than 0 a random delay is generated which is an integral multiple of the time interval. The delay of each activity is randomly generated in this fashion. The improvement process is then applied to the completed solution. The process generates the specified number of solutions and chooses the best. In the few cases we have tried, the random search process has been quite successful. With sufficient time, the number of random solutions can be set to a very large number to increase the chance of finding a good solution.

Update