|
This example comes
from a book Dynamic Programming and Markov Processes by
Ronald A. Howard, (MIT Press, Cambridge, Massachusetts, 1960).
It is a small problem that is modeled directly in the DP Solver
add-in. The following is a direct quotation from the book.
Consider the problem of a taxicab driver whose territory
encompasses three towns, A, B and C. If he is in town
A, he has three alternatives.
- He can cruise in the hope of picking up a passenger
by being hailed.
- He can drive to the nearest cab stand and wait
in line.
- He can pull over and wait for a radio call.
If he is in town C, he has the same three alternatives,
but if he is town B, the last alternative is not present
because there is no radio cab service in that town. For
a given town and a given alternative, there is a probability
that the next trip will go to each of the towns A, B
and C, and a corresponding reward in monetary units associated
with each such trip. This reward represents the income
from the trip after the necessary expenses have been
deducted. For example, in the case of alternatives 1
and 2, the cost of cruising and of driving to the nearest
stand must be included in calculating the rewards. The
probabilities of transition and the rewards depend upon
the alternative because different customer populations
will be encountered under each alternative. |
Our problem is to find the action for each state that maximizes
the average profit per trip. We will solve this problem by
directly entering the data in the DP Solver form. The probabilities
and rewards are presented as part of the data. |
Creating the Model Form |
|
|
The model is
constructed by choosing Add Model from the DP Models
add-in menu. The cab problem is a stochastic dynamic program. |
| |
|
The next dialog accepts data
describing the form of the model. The number of states, actions
and events are entered directly. The DP Solver form does not
have a change option so care must be taken to enter the correct
values. State, action and event variables are not used directly
by the procedure, but for some problems it is helpful to describe
the elements of the problem. They are used when the model is
constructed by the DP Models add-in.
The actions per state affect the number of decision list rows
are included in the form. The events per action input determines
the number of rows in the transition list. This has relevance
for the Transition Data structure.
We choose the name "Cab" for the problem and click
the Maximize Objective box. |
States |
| |
The State List is
shown below after the state names and profits have been entered,
but before the problem has been solved. The yellow colored columns
G through M hold formulas provided by the add-in. The green cells
are filled in by the computer. Here they hold the initial values. |
|
Actions and Events |
| |
|
The Action List describes the
alternatives of the cab driver. There is no direct profit
for these actions. The Event List describes the
elements of providing uncertainty. Neither the profit nor
the probabilities are completely described the events alone,
so the associated columns are irrelevant to the model. |
|
Decisions |
| |
A decision is a combination
of a state and an action. The decision list has nine entries
with three activities for each state. The transition probabilities
are in columns AH through AJ, and the transition rewards are
in columns AL though AN. The two matrices are filled with data.
The third row for city B has been assigned the NA action, because
that city has no radio service. |
| |
|
Optimization |
| |
|
The objective for the problem is to maximize
the profit per trip. The Policy method is different
for problems depending on the discount rate. With nonzero
discount rate the policy method finds the solution that
maximizes (or minimizes) the NPW of operation. With zero
discount rate, the policy method maximizes the average
profit per period (or minimizes the average cost).
|
|
| |
After three iterations
the solution is placed on the worksheet. Column J holds the
optimum policy. For each state the policy is to go to the cab
stand. Cell M14 holds the average profit with the optimum policy.
Cell N14 holds the Expected Value of the Step Values.
The policy solution with zero discount rate always results in
the equality of M14 and N14. |
|
Value Iterations |
| |
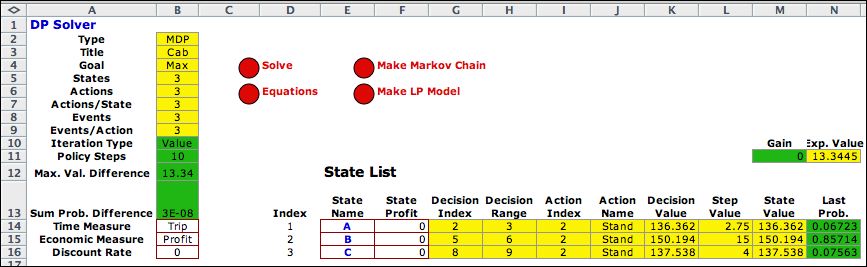
Another alternative for
the solution method is the Value Iteration. The figure
below shows the solution obtained with ten value iterations.
The solution is the optimum, but the number in B12 indicates
that the values are not converging. This will be true for any
non-transient problem with an infinite time horizon. If the discount
rate is positive, the values corresponding to the NPW will ultimately
converge, but with zero discount rate the value never converges.
The expected Step Value in N11 does converge to the
optimum value as the probability vector converges to the stead-state. |
|
| |
|



