|
The problem on this
page is to determine the optimum number of channels for a queuing
system a function of the number of customers in the system.
Because it involves both actions and uncertain transitions,
the problem is a Markov Decision Problem (MDP). The data is
created with the DP
Data add-in. The model is created by the DP Models add-in,
and the model is solved by the DP Solver add-in. Details
of the models may be found in the Queue worksheet.
A small book store has cash registers
for checking out customers. There are six registers,
however they are not always staffed. When there are only
a few customers, two registers are used. When the servers
are all busy and a waiting line grows, one or more workers
are called from other duties around the store. When called,
a worker must abandon what he or she is doing and travel
to the checkout area. This is somewhat disruptive, so
the manager would rather not open registers too often.
With added registers, the waiting line
generally diminishes. A worker can then be relieved to
return to regular duties. Sometimes however, it seems
better to keep a register open, so a sudden burst of
arrivals will not cause another call.
The manager is looking for a rational way to add
and delete operating registers. A quantitative
analysis requires a few assumptions. The busy time
for the store covers a period of 2 hours. Customers
arrive at a rate of 20 per hour and each customer requires
an average time for service of 5 minutes. Because of
limited waiting space and to reduce customer dissatisfaction,
it is determined that no more than ten customers should
be allowed wait or be in service. Any customer arriving
and finding more than 10 in service gets a $20 gift
certificate. An average customer spends $45. Open registers
are called channels, and we allow between 2 and 6 open
channels. Based on labor rates, the cost for an open
register is $10 per hour. We charge a fixed cost of
$5 whenever a register is opened and no charge if one
is closed. We evaluate the waiting time for customers
at $6 per hour.
In order to use a Markov model, it is necessary to assume
that the interarrival times and service times have exponential
distributions. The discount rate is set to 0 because
of the short interval of time involved. |
|
The Data |
| |
|
Choose the Data item from the Data
DP add-in menu to receive the dialog at the left. The
example is a finite queuing model with actions. This is the
MDP or stochastic dynamic programming problem. |
|
|
|
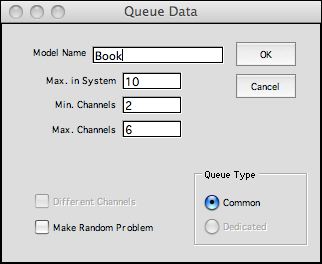
A second dialog asks for the problem
name, the maximum number of customers allowed in the system,
the minimum number of channels and the maximum number of channels.
All except the name can be changed directly on the worksheet. |
| |
Data corresponding
to the book store is entered into the MDP form below. Since
the goal is to minimize cost, the sales revenue is entered
as a negative value.
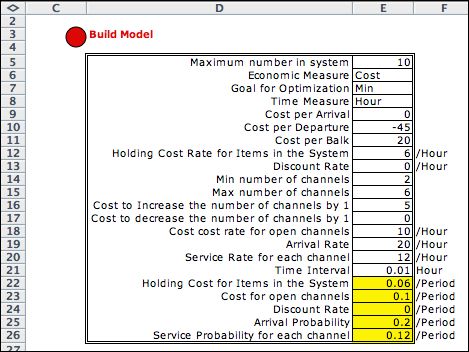
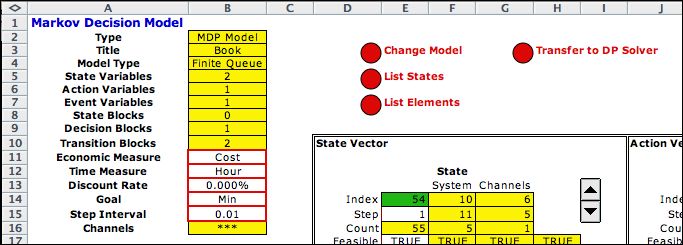
Click the Build Model button to automatically
build the DP models for this problem. The model is place on a
worksheet called Book_Model. The top of the model holds the parameters
and control buttons. Various views of the model are below.
|
States |
| |
|
The states for this system indicate the
number of customers and the number of open channels.

|
The add-in describes the state with the form shown above.
The state bounds are specified in rows 18 and 19. The cost
coefficients and the linear cost function are in row 21. |
| |
|
Clicking the List States button
at the top of the page, creates the list partly shown at
the left. There are 55 states for this problem. |
|
Actions |
| |
|
The action for this problem is to add a
channel, delete a channel or leave the channels the same.
We represent the action with a single integer variable
ranging between -1 and 1. |
|
| |
|
The action is defined for the Excel model
at the left. The cost of the action is specified in K21
with a formula that links to a data table that will be
illustrated later. |
|
| |
|
Enumeration of the action yields the action
list. |
|
Events |
| |
|
The event indicates the change in the number
in the system. A departure occurs when the service is completed.
An arrival occurs when a person enters the system. The
null event describes when there is no change. |
|
| |
|
The event is defined by the Excel model
at the left. The ranges for cost and probability
hold references to the data table. The probability of the
departure event depends on the current state of the system. |
|
| |
|
Enumeration of the event yields the event
list. |
|
Data Table |
| |
|
The table to the left is constructed to
hold the name, cost and probability data. Cells in the
model definition draw information from this table using
the Excel
Index function. The queuing system requires a
formula to compute the departure rate as a function of
the number in the system and the number of channels. This
formula is in cell AB16. |
|
Decisions |
| |
|
A decision is a combination of one state
and one action. When not all combinations are valid, decision
conditions express the logic that defines feasible decisions.
In the case of the queue, channels can be added when the
number of channels is strictly less than the maximum. This
is indicated by Decision 1.
Similarly, a channel can be deleted only if the number
of channels is strictly more than the minimum. |
The two decision conditions are modeled in Excel with two
decision blocks. The current state (6, 2) allows the action
of add (1). The first decision block indicates that the combination
is satisfied (TRUE in cell V30). Many decision combinations
will result in both blocks satisfied. The program always chooses
the block nearest the top. |
|
| |
|
There are 165 combinations of states and
actions, and 143 combinations satisfy at least one of
the decision conditions. Some are shown in the figure. |
|
Transitions |
| |
|
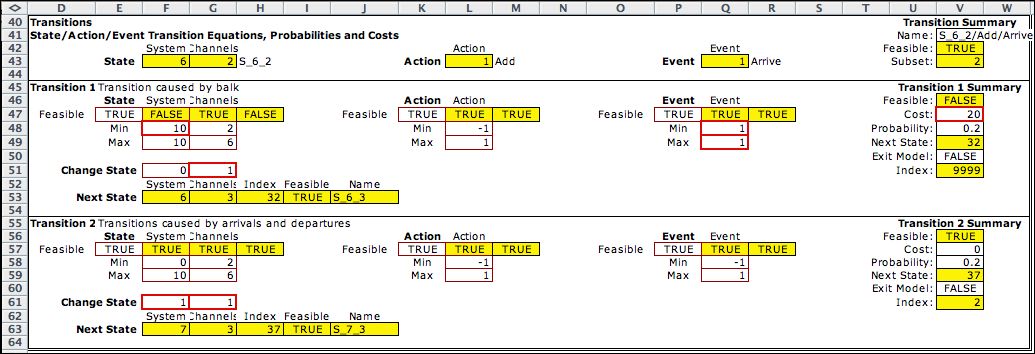
The transition determines the new state,
the probability of transition and the cost of transition.
There are two cases. The first is the balk transition that
occurs only when the number in the system is at the maximum
and when the event is an arrival. This transition carries
the cost of the balk.
The second transition is the general expression for the
remaining decision/event combinations. The first state
variable adjusts to accommodate arrival or departure events.
The second state variable adjusts to reflect channel add
and delete actions.
Only transitions to a feasible state are allowed. The
first transition takes precedence over the second.
The transitions are described by the transition section
of the model as below. |
|
 |
| |
|
There are 416 transitions defined by feasible
decisions and events. The transition probability and cost
are determined by the state, action and event combination.
The first few transitions are on the figure. |
|
The Complete DP Model |
| |
The State, Action, Event, Decision
and Transition lists comprise the complete DP model for this
problem. Clicking the Transfer to DP Solver button creates
the lists. builds a DP Solver form, and transfers the model lists
to the DP Solver form. The DP Solver model for this problem is
on the next page. |
| |
|



