Integer-Linear Programming Model (ILP)
or
Integer Programming Model (IP)
|
|
Mixed-Integer-Linear Programming Model (MILP)
or
Mixed Integer Programming Model (MIP)
|
IP Model with p strictly less than n. |
Pure Integer Programming Model |
IP with all variables required to be integer (p
= n). |
Binary Programming Model |
IP with all integer variables restricted to 0 or 1. The
model can be classified as a pure-binary programming model
or mixed-binary programming model. |
Logical Constraint |
A linear constraint involving integer variables that models
some logical condition on the decision variables. |
Concave Function of a Single Variable |
A function of a single variable with a decreasing derivative.
The figure below shows a concave function of a decision
variable. A piecewise linear approximation is shown
by the dotted lines.

A concave function in the objective function of a maximization
problem can be represented by the sum of several linear
expressions with a piecewise linear approximation (3
for the figure). No binary variables are required.
For a minimization problem, a piecewise linear approximation
requires binary variables to force the pieces to enter
the solution in the proper order. The number of binary
variables is one fewer than the number of pieces.
|
Convex Function of a Single Variable |
A function of a single variable with a increasing derivative.
The figure below shows a convex function of a decision
variable. A piecewise linear approximation is shown
by the dotted lines.
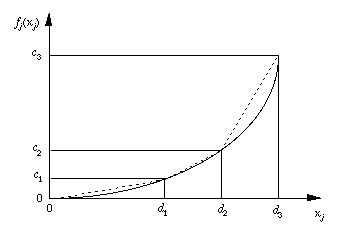
A convex function in the objective function of a minimization
problem can be represented by the sum of several linear
expressions with a piecewise linear approximation (3
for the figure). No binary variables are required.
For a maximization problem, a piecewise linear approximation
requires binary variables to force the pieces to enter
the solution in the proper order. The number of binary
variables is one fewer than the number of pieces.
|
Fixed Charge Function |
A nonlinear function that represents the cost of a
decision. The cost is 0 if the variable is 0. The cost
is a fixed value plus a cost which is linear with the
amount of the variable.
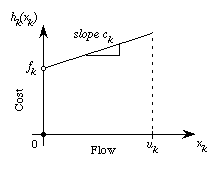
The fixed charge is modeled with a binary
variable.

The fixed charge multiplies the binary
variable and the unit cost multiplies the decision variable.

The model must include an implication
constraint that forces the decision variable to 0 when
the binary variable is zero. When the binary variable
is 1, the constraint limits the decision variable to
its upper bound. The model also includes nonnegativity
restrictions and the upper bound on the binary variable.
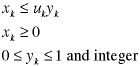
|

