
| Models |
 |
|
|
|
Resource
Allocation Problem
|
|
|
|
|
|
Resource
Allocation Problem
|

|
|
|
Statement
|
 |
The type of problem most often
identified with the application of linear program is the problem
of distributing scarce resources among alternative activities.
The Product Mix problem is a special case. In this example,
we consider a manufacturing facility that produces five different
products
using four machines.
The scarce
resources are the times available on the machines and the alternative
activities are the individual production volumes. The machine
requirements in hours per unit are shown for each product in
the table. With the exception of product 4 that does not require
machine 1, each product must pass through all four machines.
The unit profits are also shown in the table.
The facility has four machines of type 1, five of type 2,
three of type 3 and seven of type 4. Each machine operates
40 hours per week. The problem is to determine the optimum
weekly production quantities for the products. The goal is
to maximize total profit. In constructing a model, the first
step is to define the decision variables; the next step is
to write the constraints and objective function in terms of
these variables and the problem data. In the problem statement,
phrases like "at least," "no greater than," "equal
to," and "less than or equal to" imply one or
more constraints.
Machine data and processing requirements
(hrs./unit)
|
Machine |
Quantity |
Product 1 |
Product 2 |
Product 3 |
Product 4 |
Product 5 |
|
M1 |
4 |
1.2 |
1.3 |
0.7 |
0.0 |
0.5 |
|
M2 |
5 |
0.7 |
2.2 |
1.6 |
0.5 |
1.0 |
|
M3 |
3 |
0.9 |
0.7 |
1.3 |
1.0 |
0.8 |
|
M4 |
7 |
1.4 |
2.8 |
0.5 |
1.2 |
0.6 |
|
Unit profit, $ |
—— |
18 |
25 |
10 |
12 |
15 |
|
Model |
 |
Variable Definitions
Pj : quantity of
product j produced, j = 1,...,5
Machine Availability Constraints
The number of hours available on each machine type is 40 times
the number of machines. All the constraints are dimensioned
in hours. For machine 1, for example, we have 40 hrs./machine ¥ 4
machines = 160 hrs.
|
M1 : |
1.2P1 + 1.3P2 + 0.7P3 + 0.0P4 + 0.5P5 < 160 |
|
M2 : |
0.7P1 + 2.2P2 + 1.6P3 + 0.5P4 + 1.0P5 < 200 |
|
M3 : |
0.9P1 + 0.7P2 + 1.3P3 + 1.0P4 + 0.8P5 < 120 |
|
M4 : |
1.4P1 + 2.8P2 + 0.5P3 + 1.2P4 + 0.6P5 < 280 |
Nonnegativity
Pj > 0
for j = 1,...,5
Objective Function
The unit profit coefficients are given in the table. Assuming
proportionality, the profit maximization criterion can be written
as:
Maximize Z = 18P1+
25P2 + 10P3 +
12P4 + 15P5 |
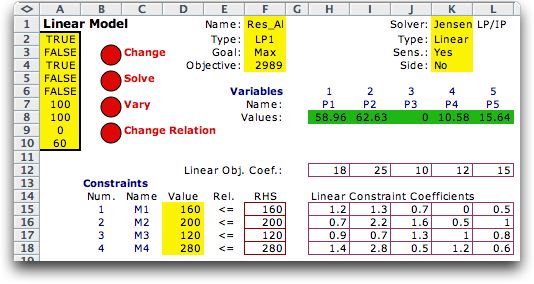
Solution |
 |
The model constructed with the
Math Programming add-in is shown below. The model has been
solved with the Jensen LP add-in. We note several things about
the solution.
- The solution is not integer. Although practical considerations
may demand that only integer quantities of the products be
manufactured, the solution to a linear programming model
is not, in general, integer. To obtain an optimum integer
answer, one must specify in the model that the variables
are to be integer. The resultant model is called an integer
programming model and is much more difficult to solve for
larger models. The analyst should report the optimal solution
as shown, and then if necessary, round the solution to integer
values. For this problem, rounding down the solution to:
P1 = 59, P2 = 62, P3 = 0, P4 = 10 and P5 = 15 will result
in a feasible solution, but the solution may not be optimal.
- The solution is basic. The simplex solution procedure used
by the Jensen LP add-in will always return a basic solution.
It will have as many basic variables as there are constraints.
As described elsewhere in this site, basic variables are
allowed to assume values that are not at their upper or lower
bounds. Since there are four constraints in this problem,
there are four basic variables, P1, P2, P4 and P5. Variable
P3 and the slack variables for the constraints are the nonbasic
variables.
- All the machine resources are bottlenecks for the optimum
solution with the hours used exactly equal to the hours available.
This is implied by the fact that the slack variables for
the constraints are all zero.
- This model does not have lower or upper bounds specified
for the variables. This is an option allowed with the Math
Programming add-in. When not specified, lower bounds on variables
are zero, and upper bounds are unlimited.
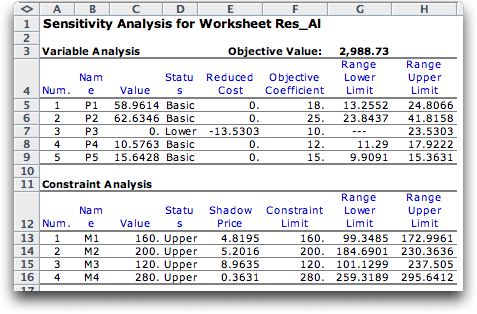
The sensitivity analysis amplifies the solution. The analysis
shows the results of changing one parameter at a time. While
a single parameter is changing, all other problem parameters
are held constant. For changes in the limits of tight constraints,
the values of the basic variables must also change so that
the equations defining the solution remain satisfied.
Variable Analysis
- The "reduced cost" column indicates the increase
in the objective function per unit change in the value of
the associated variable. The reduced costs for the basic
variables are all zero because the values of these variables
are uniquely determined by the problem parameters and cannot
be changed.
- The reduced cost of P3 indicates that if this variable
were increased from 0 to 1 the objective value (or profit)
will decrease by $13.53. It is not surprising that the reduced
cost is negative since the optimum value of P3 is zero. When
a nonbasic variable changes, the basic variables change so
that the equations defining the solution remain satisfied.
There is no information from the sensitivity analysis on
how the basic variables change or how much P3 can change
before the current basis becomes infeasible. Note that the
reduced costs are really derivatives that indicate the rate
of change. For degenerate solutions (where a basic variable
is at one of its bounds) the amount a nonbasic variable may
change before a basis change is required may actually be
zero.
- The ranges at the right of the display indicate how far
the associated objective coefficient may change before the
current solution values (P1 through P5) must change to maintain
optimality. For example, the unit profit on P1 may assume
any value between 13.26 and 24.81. The "---" used
for the lower limit of P3 indicates an indefinite lower bound.
Since P3 is zero at the optimum, reducing its unit profit
by any amount will make it even less appropriate to produce
that product.
Constraint Analysis
- A shadow price indicates the increase in the objective
value per unit increase of the associated constraint limit.
The status of all the constraints are "Upper" indicating
that the upper limits are tight. From the table we see that
increasing the hour limit of 120 for M3 increases the objective
value by the most ($8.96), while increasing the limit for
M4 increases the objective value by the least ($0.36). Again,
these quantities are rates of change. When the solution is
degenerate, no change may actually be possible.
- The ranges at the right of the display indicate how far
the limiting value may change while keeping the same optimum
basis. The shadow prices remain valid within this range.
As an example consider M1. For the solution, there are 160
hours of capacity for this machine. The capacity may range
from 99.35 hours to 173 hours while keeping the same basis
optimal. Changes above 120 cause an increase in profit of
$4.82 per unit, while changes below 120 cause a reduction
in profit by $4.82 per unit. As the value of one parameter
changes, the other parameters remain constant and the basic
variables change to keep the equations defining the solution
satisfied.
|
General Resource Allocation Model
|
| |
It is common to describe a problem
class with a general algebraic model where numeric values are
represented by lower case letters usually drawn from the early
part of the alphabet. Variables are given alphabetical representations
generally drawn from the later in the alphabet. Terms are combined
with summation signs. The general resource allocation model
is below. When the parameters are given specific numerical
values the result is an instance of the general model.
|
| |
|
|

