|
|
DECISION VARIABLES
|
Decision variables describe the quantities that the decision
makers would like to determine. They are the unknowns
of a mathematical programming model. Typically we will
determine their optimum values with an optimization method.
In a general model, decision variables are given algebraic
designations such as 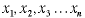 .
The number of decision variables is n, and .
The number of decision variables is n, and 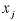 is the name of the jth variable. In a specific
situation, it is often convenient to use other names such
as
is the name of the jth variable. In a specific
situation, it is often convenient to use other names such
as 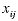 or
or 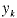 or
or 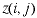 .
In computer models we use names such as FLOW1 or AB_5
to represent specific problem-related quantities. An assignment
of values to all variables in a problem is called a solution. .
In computer models we use names such as FLOW1 or AB_5
to represent specific problem-related quantities. An assignment
of values to all variables in a problem is called a solution.
|
| |
OBJECTIVE FUNCTION |
The objective function evaluates some quantitative criterion
of immediate importance such as cost, profit, utility,
or yield. The general linear objective function can be
written as
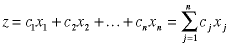
Here 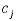 is the coefficient of the jth decision variable.
The criterion selected can be either maximized or minimized.
is the coefficient of the jth decision variable.
The criterion selected can be either maximized or minimized.
|
| |
CONSTRAINTS |
A constraint is an inequality or equality defining limitations
on decisions. Constraints arise from a variety of sources
such as limited resources, contractual obligations, or
physical laws. In general, an LP is said to have m
linear constraints that can be stated as
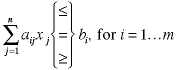
One of the three relations shown in the large brackets
must be chosen for each constraint. The number 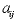 is called a "technological coefficient," and the number
is called a "technological coefficient," and the number
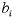 is called the "right-hand side" value of the ith
constraint. Strict inequalities (< and >) are not permitted.
When formulating a model, it is good practice to give
a name to each constraint that reflects its purpose.
is called the "right-hand side" value of the ith
constraint. Strict inequalities (< and >) are not permitted.
When formulating a model, it is good practice to give
a name to each constraint that reflects its purpose.
|
| |
SIMPLE UPPER BOUND |
Associated with each variable, 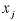 ,
may be a specified quantity, ,
may be a specified quantity, 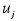 ,
that limits its value from above; ,
that limits its value from above;
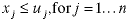
When a simple upper is not specified for a variable,
the variable is said to be unbounded from above.
|
| |
NONNEGATIVITY RESTRICTIONS |
In most practical problems the variables are required
to be nonnegative;
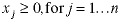
This special kind of constraint is called a nonnegativity
restriction. Sometimes variables are required to be
nonpositive or, in fact, may be unrestricted (allowing
any real value).
|
| |
COMPLETE LINEAR PROGRAMMING MODEL |
Combining the aforementioned components into a single
statement gives:
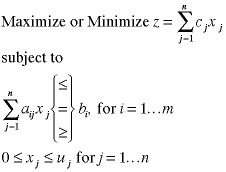
The constraints, including nonnegativity
and simple upper bounds, define the feasible region
of a problem.
|
| |
PARAMETERS |
The collection of coefficients 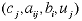 for all values of the indices i and j are
called the parameters of the model. For the model to be
completely determined all parameter values must be known.
for all values of the indices i and j are
called the parameters of the model. For the model to be
completely determined all parameter values must be known. |

