Consider a bus company scheduling drivers for
its buses. The requirement for buses varies from hour to hour
because of customer demand as shown in the figure. Time 0 on
the figure represents midnight, and times are shown with a 24
hour clock starting at midnight. For example, four buses must
run from midnight to 4 a.m., while eight buses must run from
4 a.m. until 8 a.m. We assume that the bus requirements are
the same every day.
The problem is to determine how many drivers
to schedule at each starting time to cover the requirements
for buses. Drivers work eight hour shifts that start at times:
0, 4, 8, 12, 16 or 20. For example, a driver starting at time
0 can drive a bus from time 0 to 8. A driver scheduled to
start at time 20 works for the final four hours of the day
and the first four hours of the next day. The goal is to minimize
the number of drivers used. Note that although a driver can
be hired for an eight hour period, there is no requirement
that he drive a bus for the entire period. He might be idle
for a four hour interval within the period.
One feasible solution to this problem is
to schedule 8 drivers at time 0, 10 drivers at time 8, and
12 drivers at time 16. This solution will cover all the requirements
and use a total of 30 drivers. The problem is to find the
smallest number of drivers.
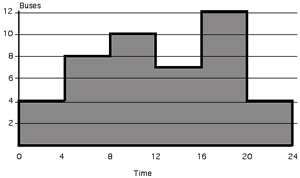
Requirements for buses in a 24 hour period

