We illustrate the analysis of the example using screen shots from the Stochastic Analysis Excel add-in. We model the ATM machine system as a continuous time Markov Chain. The CTMC section in the Computations section describes how to use the add-in for this example.

The example used here is very simple, but very complex systems can be analyzed with these techniques.

The CTMC model is defined by the rate matrix. There are six states indicating the number of customers in the system, from S0 through S5. When the system is empty (S0), the only event that can occur is for an arrival to occur. This occurs at the rate of 2 per minute. The rate is placed on the (0,1) element of the matrix indicating that the transition moves the system from S0 to S1. No other transitions are possible, so all other entries in the S0 row are zero. We are indexing the matrix from 0 to 5 to correspond to the state definitions.

When one customer is in the system, two events can occur. An arrival leads the system to S2, as indicated by the rate 2 in element (1,2). With a service completion, a customer leaves the system and the system is in S1. The rate of service is 2.5 per minute. This number is placed in element (1,0).

The rows for states 2 through 4 are constructed similarly. For S5, the system is full and an arriving customer does enter. We represent that possibility with the rate 2 in element (5,5). It is actually unimportant whether we put 0 or 2 in element (5,5).

The rate matrix is the primary model component for the CTMC. Note that the rows do not sum to 1 as do the row sums for the DTMC because the numbers in the matrix are not probabilities. They are rates. The assumption of the CTMC is that all transitions are governed by exponential distributions with parameters given in the rate matrix.

The rate matrix determines a second matrix called the Embedded DTMC Matrix. This is the DTMC that describes the steps of the process. A step occurs each time the process changes from one state to another. The times between steps have exponential distributions.

Many of the results of CTMC can be described in terms of both time and steps. We use the embedded DTMC to determine the classification of the states. For the ATM example all the states are all recurrent.

Economics

The cost data is entered on the Economics worksheet. There are two kinds of costs. The state cost is incurred during the time the process is in a state, and the transition cost is incurred when the process moves from one state to another. State costs are given as rates per unit time. The discount rate is for time value of money computations and continuous compounding is assumed. The transition cost matrix is similar to the one used for CTMC.

For the example, we assign a cost rate of 1 per minute for each customer in the system. For example with five customers in the system, cost is assigned to the system at the rate of 5 per minute.

Transient Analysis

The transient analysis describes the process in steps of the embedded DTMC. An initial state is defined in the top row of the state display. Subsequent calculations give state probabilities for each of the first 20 steps. Columns to the right of the state probabilities show expected time and cost calculations.

Since the time between each sequential pair of steps is a random variable with known probability distribution, we compute the expected time for an event to occur. For example, we see that the first step will surely lead from S0 to S1. The expected time for the step is 0.5 minutes. The subsequent computations are not easy to explain, but we see that after 20 steps, the system is expected to be almost 6 minutes into operation. Columns in the display show the cost rates (per minute) and the net present worth (NPW) computed with continuous compounding.

Clicking the More button gives 20 additional days. The Start button allows a different selection of the initial state.

Steady-State Analysis

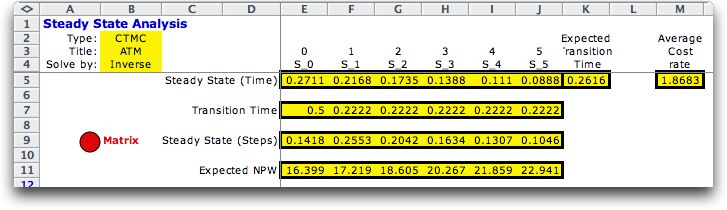
For the CTMC there are two kinds of steady state probabilities. The time-state probability for a given state is the probability that the system will be found in that state at a randomly selected time. If the time is remote from the starting time, the probability becomes independent of the initial state and converges with time to the time-steady-state probability. The first colored row (row 5) shows these probabilities for each state.

Whenever the system is in a given state, there is an expected time before the system will leave the state. These results are reported in row 7. Multiplying rows 5 and 7 together, we find the expected transition time at steady state in cell K5. A useful result is the Average Cost Rate (M5) that comes from the combination of the time-steady-state probabilities and the economic parameters.

An analysis of the embedded DTMC provides the step-steady-state probabilities. The steady state probability for state j is the limiting probability that the process is in state j after a large number of steps.

The analysis also provides the expected NPW as a function of the starting state. Most steady state results are independent of the starting state, but the NPW weighs early events more heavily than later ones, so the initial state does make a difference.

n-Step Probabilities

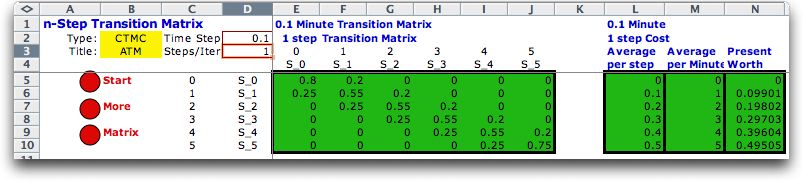
These results are obtained by discretizing time with a given step size. Cell D2 holds the time-step size of 0.1 minute for the example. Using this time, we compute the DTMC describing the transition probabilities for this time interval. The matrix is shown in the first figure below in the green cells of columns E through J. This is the 1-step transition matrix. Although all cells of the matrix below are nonzero, the accuracy of the display shows most as zero. A discretized cost analysis is shown in cells L through N.

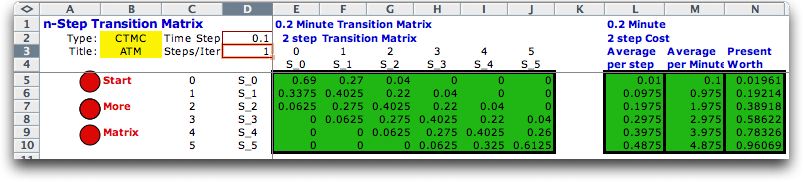
The 2-step transition matrix is the square of the 1-step matrix. Clicking the More button advances the step number to 2 and computes the 2-step transition matrix as shown in the second illustration.

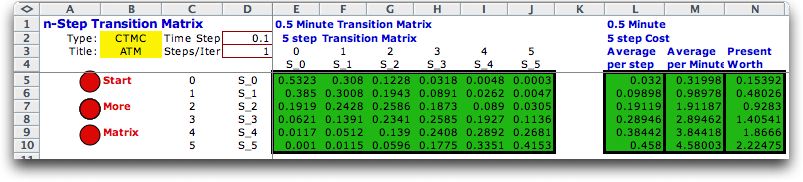
The third case shows the 5-step matrix. With more and more steps the rows of the matrix will approach the step-steady-state probabilities. For this example, five steps are equivalent to only 1/2 minute, so the system is far from steady state.

First Pass

Given some initial state it is sometimes interesting to compute the probability distribution for the number of steps required to reach some other state. The first pass analysis provides this for any two states. The example below shows the analysis for the number of steps required to pass from S0 (system empty) to S5 (system full) for the first time. The probabilities are shown in the column labeled PF(i,j,n). The first non-zero entry occurs at step 5. This first passage occurs at step 5 only if 5 consecutive customers arrive with no departures. Subsequent numbers show the cyclic nature of the system. The first occurrence of the S0-S5 transition can only occur with an odd number of events. The first 20 steps are shown in the table. The sum at the bottom of column F is the probability that the first transition occurs in the first 20 steps. We see more steps by clicking the More button. For recurrent systems the cumulative probability will approach 1.

The analysis also provides the expected number of steps required to pass for the first time from each state to the "to" state of the analysis (S5) in this case. These results start in cell J5. The expected value for first passage from S0 to S5 is about 37 steps. The table starting in row J10 shows the expected time of first passage. The expected first-passage time from S0 to S5 is about 10.5 minutes.

Simulation

To simulate the CTMC we start from some initial state and simulate the transitions from one state to the next. At any given time the system is in some state and we must simulate both the time and state of the next transition. In our analysis we simulate both events with Monte-Carlo simulation and obtain a realization of the random process. Along the way, we accumulate statistics on time, state and cost. In the example below we have already simulated 120 steps. The figure below shows the next 20 steps. The interval shown is from roughly 35 to 41 minutes. The time column shows the times of events and the state column shows the resultant states. The cost column shows the costs associated with the time interval and transition.

The cumulative cost continues to grow throughout the simulation, but we expect the cost rate and NPW to approach stead-state values.

Absorbing State Analysis

Models can be defined with multiple classes of states, where some states are transient states and some may be absorbing. Most of the results available for CTMC are determined by analyzing the embedded DTMC system.