Model Components
|
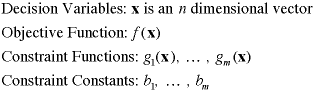
The objective and constraint functions are scalar quantities
that vary with the decision vector. The functions may
be nonlinear.
|
General Model |
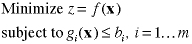
Every mathematical programming model can be put in
this form. General discussions assume this standard
format.
|
Global Minimum |
A solution that has an objective value
less than or equal to all other solutions.
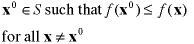
|
Unique Global Minimum |
A solution that has an objective value less than all
other solutions. Not all problems have a strict global
minimum.
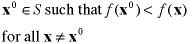
|
Weak Local Minimum |
A solution that has an objective value less than or
equal to all other solutions in a small neighborhood
of the solution.
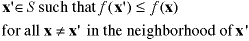
|
Strong Local Minimum
|
A solution that has an objective value less than all
other solutions in a small neighborhood of the solution.
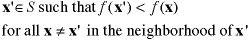
|
Global and Local Maximum |
Definitions are the same as the definitions of global
and local minimum with greater than replacing less than. |
Convex Function |
When a straight line is drawn between any two points on
a convex function, the line lies on or above the function.
The figure shows a one dimensional convex function.
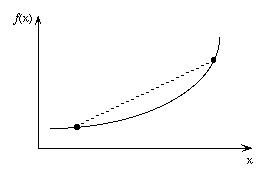
In multiple dimensions a convex function
has the following property.
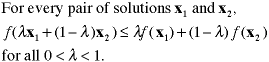
|
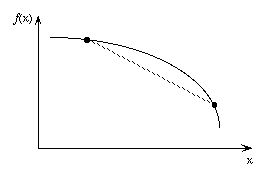
Concave Function |
When a straight line is drawn between any two points
on a concave function, the line lies on or below the
function. The figure shows a one dimensional concave
function.
In multiple dimensions a concave function
has the following property.
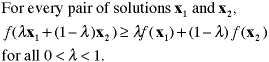
|
Feasible Region |
The feasible region is the set of all solutions that
satisfy all of the constraints.
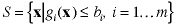
|
Convex Set |
A set S is convex if any point on the line segment
connecting any two points in the set is also in S.
The figure shows examples of convex sets in two dimensions.
An important issue in nonlinear programming is whether
the feasible region is convex.
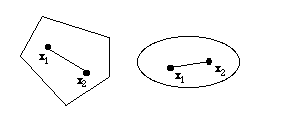
When the all the constraints of a problem
are linear or convex, the feasible region is a convex
set.
If the objective function is a convex
and the feasible region defines a convex set, every
local minimum is a global minimum.
If the objective function is not a convex
function, a local minima may or may not be global minimum.
A nonlinear programming algorithm may terminate at a
solution that is not a global minimum.
|
Nonconvex Set |
If a set does not satisfy the requirements of convex set,
it is a nonconvex set. The figure shows examples of nonconvex
sets in two dimensions.
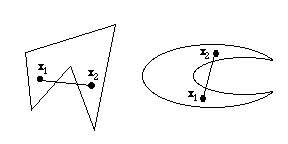
If the feasible region of a problem is
a nonconvex set, a local minimum may or may not be global
minimum. A nonlinear programming algorithm may terminate
at a solution that is not a global minimum.
|

