|
|
|
|
ATM
Example
|

|
|
|
|
To illustrate the components of
a stochastic process, we use the example of a single automated
teller machine (ATM) located in foyer of a bank. The
ATM performs banking operations for arriving customers. Only
one person at a time can use the machine and that person is
said to be in service. Other
customers arriving when the machine is busy must wait in a
single queue; these persons are said to be in the queue.
Following the rule of first-come-first-served and
assuming that the average arrival rate is less than the
average service rate, a person in the queue will eventually
step up to the ATM, execute a series of transactions,
and then leave the system. The number of persons
in the system at any point in time is the sum of the
number in service and the number in the queue.
|
Time |
| |
Many situations are conveniently
described by a sequence of events that occur over time. For
example, the number of persons (in the queue or in service)
in front of the ATM depends on the particular sequence of arrivals
and departures.
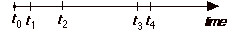
Events occurring in continuous time
In the figure, time is a treated as a continuous parameter
but events occur at specific instances. We use t to
represent time and use subscripts to identify the specific
instances.
|
State |
| |
The state describes the attributes
of a system at some point in time. For the ATM, the state
indicates the number of persons in the system (either in service
or in the queue). It may be limited to a maximum value
determined by the physical size of the bank foyer or it may
be unlimited for practical purposes if a line is allowed to
form outside the building. The minimum number is of course
zero, occurring when there are no customers in service. In
this case, the machine is said to be idle.
Depending on the situation, the state may be very complex
or very simple. To provide for this variety, we use an m-component
vector,
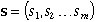
to describe the state. The ATM example allows a simple
state definition with only one dimension.
Here
s = (n)
where n is the number in the system. To speak
of the state at time 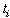 ,
we attach the subscript i to the state vector to get ,
we attach the subscript i to the state vector to get 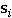 . .
It is often convenient to assign a unique nonnegative integer
index to each possible value of the state vector.
We call this X and require that for each s there
is a unique value of X.
For the ATM example, an obvious assignment is X = n.
For more complex state definitions there may be several possible
assignments describing different characteristics of the system. X(t) is
the value of the variable at time t.
Because of the random nature of a stochastic process, the future
realization of X(t) is usually not predictable
with certainty. Rather X(t) is a random
variable. To understand the behavior of the system under
study, it is necessary to describe the statistical properties
of this random variable.
The set of all possible states is called the state space and
is denoted by S. In general, a state space
may be either continuous or discrete but here we limit our
attention the discrete case only.
For the ATM example, the set of all nonnegative integers can
be used to describe the number of persons in the system at
any instance, so
S = {0, 1, 2,...}.
This is an infinite state space and assumes that there is
no limit to the number of persons that can be in the system. If
the physical dimensions of the bank foyer restrict the number
of customers to a maximum K, the state space is finite,
and
S = {0, 1, 2,...,K}. |
Activities and Events |
| |
The dynamic nature of a system
is evidenced by its activities.
Each activity has some time interval between its initiation and
completion, called the duration. An activity culminates
in an event. In the ATM example there are
two activities, one associated with service and the other with
arrivals. The service activity begins when a customer first appears
in front of the ATM and ends when all her banking transactions
are completed and she departs. This event is typically
referred to as a service completion. The duration
of the activity that leads to this event is the time for service.
The arrival activity begins immediately after a customer arrives
and ends with the arrival of the next customer.
The event is an arrival and the duration of the accompanying
activity is the time between arrivals.
Symbolically, we use letters to designate activities and events. Because
each activity leads to a unique event, we use the same letter
for both the activity and the subsequent event. For the
current example, a is used to represent the arrival
activity as well as the event of an arrival, and d to
represent the service activity as well as the event of service
completion (and departure of the customer).
The duration of each activity is a random variable governed
by a probability distribution. This is the probabilistic
element of the stochastic process. The time for service, 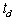 ,
and the time between arrivals, ,
and the time between arrivals, 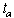 ,
may be described by their respective cumulative distribution
functions ,
may be described by their respective cumulative distribution
functions
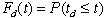 and and 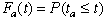 .. ..
Generally speaking, the set of possible activities, and thus
the set of possible events, depends on the state of the system. For
example, when there are no customers in the system, the service
activity is not active and no departure can occur. If
there is some upper limit on the number of customers that can
wait in the queue, no arrival can occur when the queue is full. We
use the notation Y(s) to describe the
set of possible activities (events) for state s.
For the ATM example, we have
Y(0) = {a}; Y(n)
= {a, d} when 0 < n < K; Y(K)
= {d}.
The cardinality of Y(s) may be infinite
or finite, depending on the situation. In what follows,
the term calendar is used to describe Y(s).
The set of activities that may occur while in state s determines
the calendar for the state.
Given the current state s, one of the events in Y(s)
will occur next. This next event and the time
it takes place have important effects on the state of the system. Let x be
the next event and 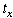 be
the time that it occurs. When the activity durations
are random variables, x and be
the time that it occurs. When the activity durations
are random variables, x and 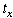 are
random variables. By definition, are
random variables. By definition,
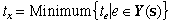
where x is the event for which the minimum is obtained. |
Transition |
| |
A transition is caused by an event
and results in movement from one state to another. Thus
it always relates to two states. For convenience we will
say that a transition describes the movement from the current state
to the next state. There are cases, however, in
which the current state is allowed to be the same as the next
state.
A state-transition network is used to describe the components
of the stochastic model. In the diagram, each state is
represented by a node and the possible transitions by directed
arcs. Each arc originates at one state and terminates
at another. The event leading to the transition is shown
adjacent to the arc. The figure depicts the network for
the ATM example.
An arrival causes a transition to the next higher state, and
a departure causes a transition to the next lower state.
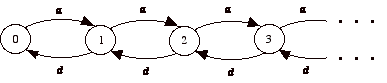
State-transition network for ATM example
When the stochastic process is relatively simple,
the transitions can be represented graphically as in the figure. For
complex situations we use a transition function.
This function gives the value of the next state in terms of
the current state and the next event. Let the current
state be s and the next event be x. Let s'
be the next state determined by the transition function T(s,x),
such that
s'
= T(s,x).
When the state vector has more than one component, the transition
function is multidimensional. It describes how each component
of the state vector changes when the event occurs.
For the ATM example, the transition equation is
s' = s +
1 if x = a and
s' = s -
1 if x = d. |
The Process |
| |
The state, the activity and event
definitions, the probability distributions for activity durations,
and the state-transition network are sufficient to describe
a stochastic process.
In more formal terms, we have the following.
Definition 1: A stochastic process is a collection
of random variables {X(t)},
where t is a
time index that takes values from a given set T.
Both X(t)
and T may be continuous or discrete, giving rise to four different
categories of models. We consider here only finite discrete
state space ( X(t) is
finite and discrete). Both continuous and discrete time models
are considered.
A Markov process is a special case of a stochastic process
in which all the information concerning the model is entirely
determined by the current state. It is often said to
be memoryless because the future realization depends only on
the current state and in no way on the past.
Definition 2: Markovian property - Given that the
current state is known, the conditional probability of the
next state is independent of the states traversed prior to
the current state. |
| |
|
|

