The Gamma distribution models a random variable that is restricted to nonnegative values. The general form has two positive parameters r and determining the density function. We restrict attention to integer values of r although the Gamma distribution is defined for noninteger values as well.

The figure shows several Gamma distributions for different parameter values. The distribution allows only positive values and is skewed to the right. There is no upper limit on the value of the random variable. The parameter r has the greatest affect on the shape of the distribution. With r equal to 1, the distribution is the exponential distribution. As r increases, the mode moves away from the origin, and the distribution becomes more peaked and symmetrical. As r increases, the distribution approaches the Normal distribution.

The Gamma distribution is used to model the time required to perform some operation. The parameter primarily affects the location of the distribution. When r is integer, the distribution is often called the Erlang distribution. This is the distribution of the sum of r exponentially distributed random variables each with mean 1/. This distribution is often used to model a service operation comprised of a series of individual steps. The closed form expression for F(x) is available for the Erlang distribution and it is shown above.

Example

Example: Consider a simple manufacturing operation whose completion time has a mean equal to 10 minutes. We ask, what is the probability that the completion time will not exceed 11 minutes? We first investigate this question assuming the time has an Exponential distribution (a special case of the gamma), then we divide the operation into several steps, each with an exponential distribution.

When the operation is performed in one step, we use the exponential distribution with =1/10. The add-in computes the probability as 0.667.

Now assume that we can divide the operation into two steps such that each step has a mean time for completion of 5 minutes and the steps are done in sequence. In this situation, the total completion time has a gamma (or Erlang) distribution with r = 2 and = 0.2.

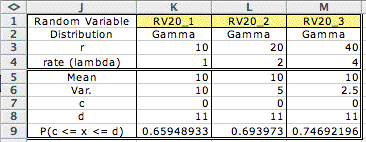
Continuing in this fashion for different values of r with = r / 10, gives the results below. As r increases, the distribution has less variance and the probability of completing the operation in 11 minutes increases.