|
The MDP model uses
the DP
Solver to find solutions. The figure below shows the
final solution. This is the steady-state solution obtained
with the policy-interation method. Columns
K and L hold the optimum policies for each state. Column
O holds the total prizes associated with starting in each
state. After state (0,0) and excepting state (3,3), the values
are all slightly less than 1 because of the small penalties
for using the blocking actions. |
|
| |
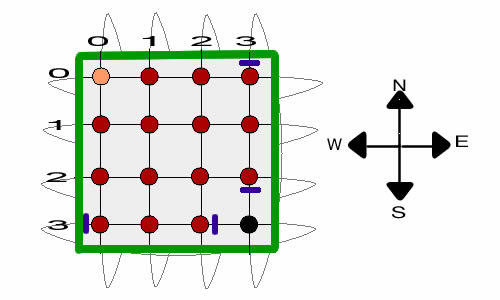
The optimum solution
blocks all transitions into state (3,3).
|
| |
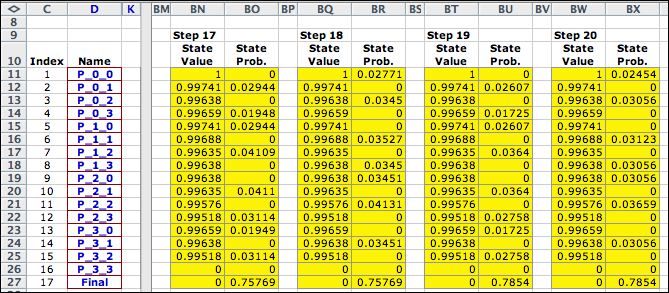
Fixing the solution at the optimum,
we performed 20 value iterations with the walker starting at
(3,0). As the steps progress, more and more probability gets
harvested at the final state (0,0). |
|
| |
After 20 steps almost 80% of
the probability is at the final state. Eventually the final
state will have almost all the probability. Not considering
the final state, the system has the characteristic of a transient
MDP.
|
| |
A Markov Chain analysis of the optimum
solution shows that the expected number of steps for the system
to reach the final state from state (3,0) is 13.25. The path to
the final state passes through the exit state (0,0) |
| |
|
Discounting the Prize |
| |
The example to this point has the
goal of minimizing the probability that the walker reaches the
cell (3,3). The solution accomplishes that very well by using
four doors to obtain a zero probability. With a nonzero discount
factor, the prize loses value at each step that does not reach
the state (0,0). When the discount rate is greater than 0, the
tendency would be place doors in a manner that hurries the collection
of the prize.
We modify the example to introduce a discount rate
of 1% per step. All the move penalties are set to zero so as
not to confuse the effects of the discount factor with the
penalty. After 20 value iterations, the solution of the revised
problem is below. |
| |
|
| |
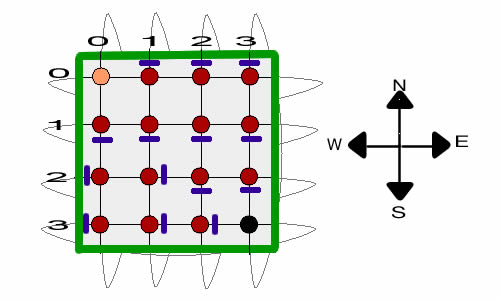
The solution has a blocking action
for every state except the two exit states. The probabilities
shown in column P are the state probabilities after 20 steps
starting from state (3,0). Over 93% of the probability has
reach the final state compared to 78% with no discounting.
|
| |
Subsequent evaluation of the
first passage times reveals that the first passage times to
the final state are reduced for all starting states. In particular
the expected first passage time for the state (3,0) is reduced
to 8 from its value of 13.25 without discounting.

|
Summary |
| |
This page has demonstrated a
MDP model for the random walk. Inspired by the work of Dimitrov
and Morton, we have constructed the blocking action
for the MDP. Answers comparable to those of the paper were obtained
using our Excel add-ins. |
| |
|



