|
|
 |
Dynamic
Programming
Examples |
 |
-
Revenue Management Model |
|
Revenue management
is one of the successful applications of operations research.
It is used throughout the transportation industry and could
be valuable whenever a business has a fixed capacity resource
that is used on a regular schedule. Examples are airline flights,
hotel accommodations, batch processing machines and many others.
All these examples require a major fixed cost for providing
a service. The cost is independent of the number of customers
who pay to use the service. To maximize profit, the business
wants as many customers as possible who individually pay a
high price for the service. In most cases there is tradeoff
between these goals. The maximum number of customers can only
be obtained with a low unit price, and the highest unit price
results in the fewest customers. Since the cost is fixed, the
goal is to find the combination of pricing and customer demand
to maximize total revenue. This problem is addressed through
revenue management. The example on this page is one of the
simplest of the revenue management problems.
An example is an airplane used in a commercial setting.
A small airline runs flights between
several small cities, and this problem considers a single
flight from one city to another. The plane flies a
weekly schedule between the two cities and has
a capacity of 20 passengers. For some time the airline
has operated using a fixed price per ticket of $120.
The cost of operating the flight including capital investment,
fuel, pilots, and stewards is $1,800. When
the plane is full, the revenue for the flight is $2,400,
so the airline clears a profit of $600. Unfortunately,
because of an economic downturn, the plane
has been carrying an average of only 14 passengers. This
yields a revenue of $1,680 for a net loss of
$120 per flight. Since the costs are fixed, the best
way to increase profit would be to sell more
tickets and increase the revenue per flight. |
The commodity for sale is
an airplane seat. Although every seat performs the same
function of carrying a customer from one city to the other,
various benefits can be made available to allow some seats
to be priced higher than others. Benefits include early
check-in, free drinks, pillows or blankets. Lower priced seats
do not enjoy these perks and are more restricted. Restrictions
include the inability to change or cancel the reservation
or the requirement to stay at the destination city over Saturday
night. Some tickets might be offered at lower prices just before
the flight. Selling a ticket for a seat that would otherwise
be empty always increases the total revenue.
In some manner, the market for the product
must be segmented into several classes: 1, 2, … m.
The classes have different prices with the price
decreasing with increasing class index.

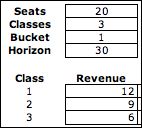 |
The data at the left is used as an example.
The capacity of the plane is 20 and there are three price
classes. Time is divided into buckets, here defined to
be one day long. Tickets
are available 30
days before the flight leaves (the Horizon). |
|
Reservations |
|
The flight
leaves at a scheduled clock time. We divide the time before
the plane leaves into equal intervals called buckets.
The buckets are numbered to indicate the number
of buckets before the plane leaves. The plane leaves at time
0. One day before departure is time 1, and so on. N is
the number of time buckets between when the airline begins
to sell tickets and when the plane leaves.

Customers make reservations
though the internet. To control the number of customers
that will be accepted from each class, each time bucket is
assigned a class number that indicates the maximum class
index that is acceptable.
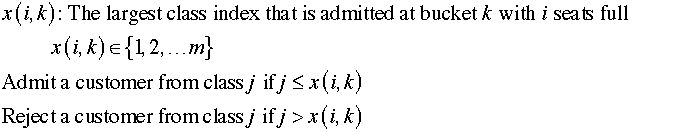
For this problem we assume that only one reservation
is booked during a time bucket. Customers in the different
classes arrive independently at random times described by a
Poisson process. The action is to specify the value of x for
each state in each time bucket. We
assume that the first acceptable customer that arrives during
a bucket is booked.
Customers arriving later than the first in a bucket are lost.
This may seem to be an unrealistic assumption, but the model
can be made more accurate with smaller duration buckets.
The chart below shows one solution for the problem. The horizontal
axis is the number of days until the flight departure.
The vertical axis is the number of seats that are full. The colored
cells indicate the policy for each combination. For green cells,
reservations are accepted for all three classes. In yellow cells,
reservations are allowed for classes 1 and 2.
Only class 1 is accepted in the red cells.
A solution like the one shown is reasonable. When there is only
day to go, empty seats should be sold for any price, since a
seat not sold provides zero revenue. At earlier times when
only a few seats are left, it is better to restrict reservations
to make sure there is opportunity for higher paying customers
to buy seats. Early in the reservation process, it is better
not to sell the cheaper tickets so that space will
be available if more expensive tickets are requested later. No reservations
are accepted when the state reaches the capacity of the plane. |
|
| |
In the MDP model the state
variable is the number of booked seats, and the stage variable
is the time bucket index. The
chart shows the optimum actions. For
bucket 1 the decision is 3 for all states less than 20, the
capacity of the plane. For bucket 2, the decision is to accept
reservations of all types unless the state is 19, one less
than the capacity. In state 19 we book only classes 1 or 2.
In bucket 30, reservations begin with no seats booked, no reservations
are accepted at price 3.
The time between arrivals
for each class is assumed to be exponentially distributed.
Different classes have different arrival rates. The exponential
assumption allows computation of the probability that no acceptable
arrival occurs during the time bucket and the probability of
booking a customer from each acceptable class. For this model
we assume that arrival rates are independent of time, so the
parameters are not indexed by the bucket number. This means
that the model is homogeneous in time.

The decision problem is to assign a class
index to each state and each time bucket. No reservations are
accepted for classes with indices at above the maximum. The
goal is to maximize the expected total revenue over the time
horizon. |
Model |
| |
We model this problem as
a Markov decision process (MDP). The number of seats taken
is the state variable. The stage variable is the bucket index.
Since the model for each stage is the same, the stage variable
does not appear in the model formulation. You will see that
the effect of time is considered by the computational process
of solving the model. The action is the selection of the maximum
class index to admit. The event is the index of the class of
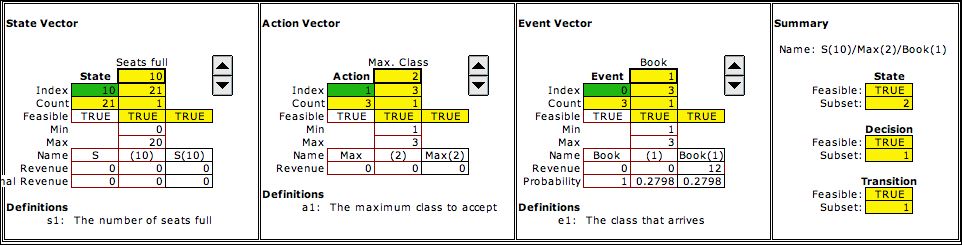
the arriving customer. The figure shows the state,
action and event variables defined on the DP model worksheet.

|
 |
| |
The example shows the model
with 10 seats full, the action is to accept reservations of
class 1 or 2, and the event indicates that a customer of class
1 has arrived during the interval. The ticket is booked. The
event element holds formulas that describe the revenue and
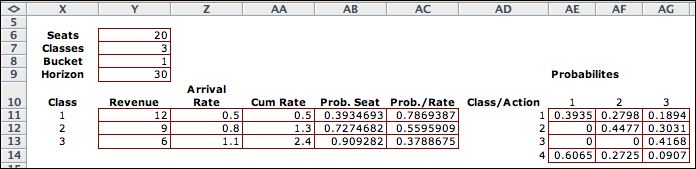
probability associated with the event. These formulas link
to a data table constructed to the right of the model and illustrated
below. Changing this data automatically changes the related
cells of the model.
The event of no arrival is modeled implicitly.
When the DP Models add-in creates the model, it automatically
creates a null event that holds all unspecified probability
for a given state/action combination. This null event represents
the situation when no acceptable class arrives during a time
bucket. |
States |
| |
The state variable ranges from 0
to the capacity. The first state set indicates that state 20
is an exit state. No customers are added after the plane is full.
The second set covers all the other states. |
 |
Transitions |
| |
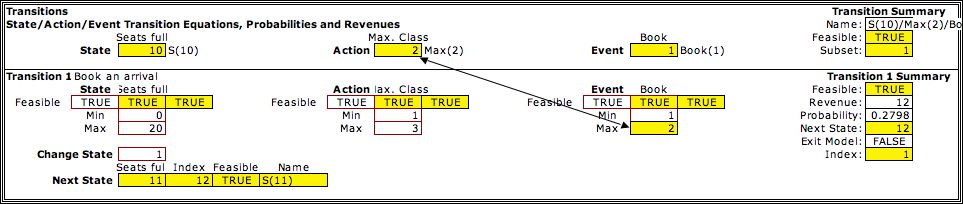
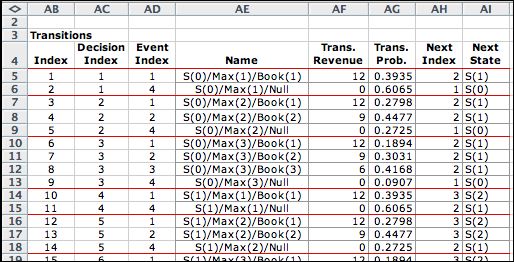
A single transition block advances
the state variable by 1 when an acceptable customer is booked.
The constant 1 is placed in the Change State cell. The
maximum event cell is set equal to the action variable. During
the model generation, whenever a state/action/event
combination satisfies the bounds on the elements, a transition
is created. The figure shows the transition from state 10 to
state 11 when the action is 2 and the event is 1. A class 1 customer
arrives and is booked. The revenue from the event in the summary
column is 12 and the probability is 0.2798. The revenue
and probability are computed in the event element. |
 |
Lists |
| |
When the add-in is called to generate
the solver model, five lists are created as shown below.
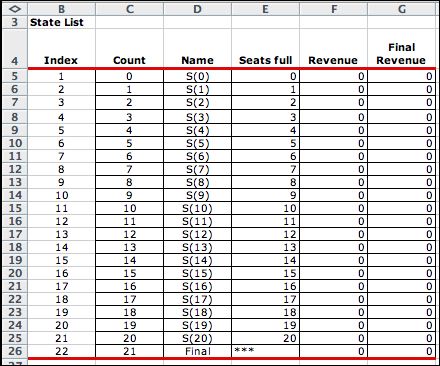 |
The state list shows all possible states for
the system. A Final state is necessary for the transition
from state 20 to the exit. |
|
The three actions are to set the maximum acceptance index
to 1, 2 or 3. |
|
The event list shows the classes that might be booked during
the time bucket. |
.
|
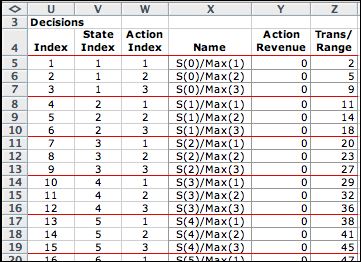
There are 62 state/action combinations, or decisions, that
are feasible for the model. State 20 allows
only the Null action. |
.
|
There are 182 transitions for this model. The transitions
carry the revenue and probability information. |
|
Optimization |
| |
Clicking the Transfer to DP Solver creates
the five lists and transfers them to the solver model
worksheet. The solution is on the next page. |
|
| |
|
|



