|
|
 |
Dynamic
Programming
Examples |
 |
-
Sequence Model |
|
This example describes
a sequencing problem for a set of wells in an off-shore oil
field. We use it here to show the possibility of solving sequencing
problems with dynamic programming. The problem is addressed
in the paper: Optimal
Sequential Exploration: A Binary Learning Model, by J.
Eric Bickel and James E. Smith, Decision Analysis, Vol 3, No.
1, March 2006. The complete problem description, the model
and the solution technique are found the paper. Here we concentrate
on solving the stochastic DP using Excel. We
use the DP Models add-in to build the model. The model is
solved with the DP solver add-in. The solution obtained with
the add-in is the same as the solution given in the paper. |
Problem Description |
| |
The following is
a copy of the first paragraph of the paper that provides an
introduction to the topic.
| "The motivation for this paper began with a consulting
engagement for a client that wanted to prioritize
its deep-water oil and gas exploration program.
The client had grouped the oil and gas prospects
into clusters it believed to be geologically dependent
and wanted to understand how the results for one
well change the chance of success for the remaining
undrilled prospects and how this information
should affect the drilling strategy. Given that the
wells cost tens of millions of dollars to drill, an
optimal drilling program could generate significant
savings and make an otherwise unattractive exploration
opportunity economically viable. Researchers
exploring multiple related R&D projects face similar
problems—given dependent projects, which projects
should they pursue first?" |
In the following we deal with the problem of sequencing the
drilling of six wells. We characterize a successful well as wet,
and an unsuccessful well as dry. Data concerning the
wells is in Table 1. The Include column indicates
whether a particular well should be included in the sequence.
The p column
indicates the marginal (unconditioned on the sequence) probability
that the well will be wet. The EV|wet column
provides the expected net present worth of the cash flow of
a wet well, where the present worth value is computed at the
time of drilling. The EV/dry column
is the expected net present worth of a dry well. Since no future
cash flows are projected from a dry well, this is the cost
of drilling. The EV column
is expected return for the well considered alone from the other
wells. It is, computed by the formula:
EV = (p)*EV|wet + (1 - p)*EV|dry
Table
1. Example Well Data |
Well |
Include |
p |
EV|wet |
EV|dry |
EV |
1 |
1 |
0.35 |
60.00 |
-35.00 |
-1.75 |
2 |
1 |
0.49 |
15.00 |
-20.00 |
-2.85 |
3 |
1 |
0.53 |
30.00 |
-35.00 |
-0.55 |
4 |
1 |
0.83 |
8.00 |
-40.00 |
-0.16 |
5 |
1 |
0.33 |
40.00 |
-20.00 |
-0.20 |
6 |
1 |
0.18 |
80.00 |
-20.00 |
-2.00 |
In this problem we have the choice of drilling the well or not.
Based on the EV values in the table, none of the wells should
be drilled. There may be benefits to considering the wells in order,
however. When
wells are drilled in sequence, the probabilities of wet or dry
of a particular well may be affected by the success or failure
of wells drilled earlier in the sequence.
Estimating the conditional probabilities is
a major topic of the Bickel/Smith paper, but here we do not attempt
to explain it. Through a series of questions to company experts,
the researchers were able to compute the joint probabilities
of complete scenarios. These are repeated
from the paper in the table below. A scenario indicates the results
for all six wells. Each scenario is described by a vector of
6 binary variables, with 1 indicating a wet well and 0 a dry
well. For example one scenario is that all six wells are dry
as shown as the first entry of the list , (0, 0, 0,
0, 0, 0). The probability of this scenario is estimated by the
methods in the paper to be 0.0343. There are 2^6 or 64 scenarios.
We seek a sequence of drilling the wells that yields the maximum
expected net present worth of oil field. The solution is not
a deterministic sequence that is specified before any wills are
drilled. Rather, the solution is a sequential decision rule that
specifies the next well to drill, given the results for the wells
drilling previously. This is called a policy. For example, if
the policy is to drill 3 first, the next well in the sequence
depends on whether well 3 is wet or dry. If it well 3 is wet,
the next well to drill might be well 6. If well 3 is dry, the
policy might be to abandon the field and drill no more wells.
To find the optimum policy we use stochastic dynamic programming.
We first use the DP Models add-in to model the problem, and then
use the DP Solver add-into find the solution. We use the table
below to find event probabilities. |
|
|
|
Dynamic Programming Model |
| |
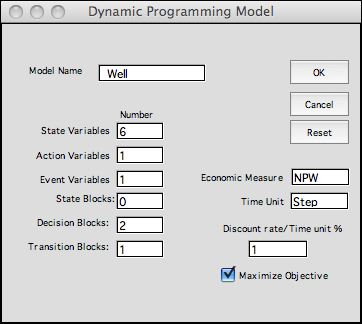 |
To create the DP model, select Add Models from
the DP Models menu. On the ensuing dialog choose the MDP option.
That presents the dialog to the left. The model consists
of states defined by six state variables, one action variable
and one event variable. We discuss the elements below. |
|
Model Elements |
| |
|
The state
definition has six variables corresponding to the six wells.
Each variable takes on three values, -1, 0 and 1. The value
-1 indicates that the well has not yet been drilled. The
0 value means that the well has been drilled and found
to be dry. The 1 value means that the well has been drilled
and found to be wet. The count row indicates that there
are 729 feasible state vectors.
Cell E17 holds logical conditions that determine if a
given state is feasible. For this problem only the variable
bounds determine feasibility, so cell
E17 is set to TRUE.
The range labeled Include is provided to restrict
the wells to be considered. A value of 0 would indicate
that the associated well would not be drilled. All wells
are included for this example. State names are determined
in cell L20. An underline indicates that the well has not
been drilled and 0 and 1 are used to show the results of
drilling.
States do not affect the objective value directly so row
21 has all zeros. |
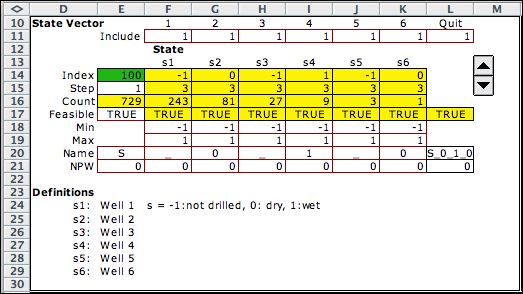 |
A second state is shown for comparison. The states are
enumerated by changing the index in E14. Each integer value
represents a state. The index of 100 determines the state
with wells 1, 3, and 5 not drilled. Well 2 is dry, well
4 is wet, and well 6 is dry. |
|
The action is described a single variable specifying
the next well to drill. The example selects well 3. A value
of 7 indicates that drilling is abandoned.
The enumeration includes all 7 values of the action variable,
but a logical expression in the feasibility cell (O17)
restricts actions to the set of wells included in the problem
and specified in the range F11:L11. The logical expression
in O17 is:
=INDEX(F11:L11,1,Well_DPM_Action)=1
The result is TRUE when the entry in the
range corresponding to the action is equal to 1.
Otherwise it is FALSE.
Again the action has no direct effect on
the NPW. |
|
The event vector has only two values, 0 representing
dry and 1 representing wet. The event holds the NPW contribution
and probability associated with the result. The NPW is the
value at the time of drilling. The transition equations will
further discount the value to the beginning of the study
period.
The probability of the wet result is computed from
the scenario probabilities given in the table above. It
is the probability of success of the well given the results
of all drilling that occurred earlier in the sequence.
The probability does not depend on the sequence of the wells,
only on the set of drilled wells and whether they were
wet or dry. This information is provided by the state variable.
The example shown is for the state with no drilled wells,
so the probability of the wet result for well 3 is simply
the marginal probability from table 1. The NPW contribution
is from Table 1. |
|
The same event for the state S_0_1_0 is shown at the left.
Note that the conditional probability of well 3 being wet
has been changed by the state. This probability depends on
the scenario probability data given earlier. The formulas
providing this result are on the worksheet for this example. |
|
| |
|
Clicking the List States button
at the top of the page, creates the list shown in part
to the left. Including the Final state
at the bottom of the list there are 730 entries on the
list.
This list and all the other lists described on this page
are on the worksheet named Well Lists. |
|
Decisions |
| |
Two decision subsets are defined
in the model. The first describes the set of actions regarding
drilling a well, as indicated by the upper bound of 6 on the
action variable for the Decision 1 subset. The logical cell
O39 is interesting because it only allows actions on wells
not yet drilled. The logical expression implementing this is:
=INDEX(F35:L35,Well_DPM_DecAction)=-1
The range (F35:L35) holds the state vector plus a cell that
represents the Quit decision. Cell P35 has the name
"Well_DPM_DecAction". The expression allows only
wells that have a -1 in the corresponding state vector. Cell
L35 is included so the expression will not generate an error
for action 7, Quit. Errors occurring with the INDEX function
cause the program to prematurely terminate.
The second Decision subset is only for action 7, Quit. That
action is identified as an Exit state with the value
TRUE in Z46. |
 |
| |
|
Clicking the List Elements button
at the top of the page, creates the Decision and Transition lists.
The decision list combines feasible states
with feasible actions to obtain feasible decisions. The
first six decisions are for the state with no wells drilled.
As drilling results are added, the number of feasible decisions
decrease. There are 2188 decisions for this model. |
|
Transitions |
| |
The transitions move the system
from the current state to a new state. The new state
depends on the current state, the action, and the event. The
transition is affected through the Change
State range
in row 61. The equation in cell F61, refers to the action and
event. When the cell represents the current action, the state
is changed by adding +2 for a wet well and +1 for a dry well.
The formula uses the Excel IF function.
=IF(Well_DPM_TransAction=F60,Well_DPM_TransEvent+1,0)
The objective term is reflected in cell Z57 and the probability
of the event is in Z58. |
|
| |
|
The program combines all feasible decisions
with each of the event possibilities to obtain the Transition
List. The first few and last few transitions are
shown at the left. There are 3646 feasible transitions. |
|
| |
We see at the end of
the list, the Final State. The final state has a transition that
returns to itself. Except for the final state the transitions
from all states go to a state with a greater index. This kind
of state network is called an acyclic network because there
can be no cycle leading from one state back to itself. |
Summary |
| |
This particular model is for the well sequencing
problem, but many of its features could be adapted to other
sequencing problems. It is a fairly large problem for our Excel
DP Solver, but once constructed it is solved readily. We discuss
the solution on the next page.
|
| |
|
|



