|
The solution of
the well sequencing problem is found with the DP Solver add-in
(dp_solver.xla). Click the Transfer
to DP Solver at
the top of the model page. Of the Solver forms, only
the Transition List option is possible. The number
of states is too large for either matrix format. The add-in
automatically constructs the solver model. To find the optimum
solution, click the Solve button
at the top of the page. |
| |
|
We choose the Value approach
for optimization. This number of states is too large for
the Policy option.
The Acyclic option could have been chosen since
the network for this problem is acyclic. The Value option
improves the policy at each iteration. It stops when two
solutions have almost the same values. Since this problem
is transient, it will terminate in a finite number of iterations. |
|
| |
After five iterations, the optimum
is found. Part
of the solver worksheet is shown below for only a few of the
730 states. Starting in state 1, the optimum
solution is to drill well 3. The State Value is the
optimum value for the sequencing problem, 14.40296 millions.
It is apparent that some drilling is recommended for this field
even through the valuation of the individual wells are all less
than zero. |
|
| |
The remaining decisions
of the sequence problem depend on the outcome of drilling well
3. |
Recovering the Solution |
|
A major stumbling block for
stochastic dynamic programming is in recovering the optimum
solution. Even when the system starts in a particular state,
the uncertainty associated with transitions quickly brings
other states into the solution. This problem is not so apparent
in deterministic DP because the solution is usually a single
path through the state space, and recovering that path is not
too difficult.
The tables on the DP solution page completely describe all
states and all transitions, so theoretically the states entering
the solution can be discovered by tracing through the various tables.
For example, starting at state 1 with no wells drilled, the state
table reveals that the optimum decision index is 3. This information
is in column M of the first row. |
|
| |
From row 3 of the decision list
we see that the solution involves drilling well 3, and the
information regarding transitions is in column AM. The numbers
in column AM give the last row of the transition list
that pertains to the decision. For decision 3 we see that the
transitions for decision 3 are in rows 5 and 6. The starting
row is one greater that the last row for decision 2. |
|
| |
Moving to rows 5 and 6 of the transition
list we see that two transitions are defined, one for the dry result
and one for the wet result. The transition probabilities
for these events are in column AY. The next state for a transition
is in column AZ, the dry transition is to state 28, and the
wet transition is to state 55. |
|
| |
The recovery process then returns
to the state list to review states 28 and 55.
The decisions in these states lead to yet other states in the
solution. This recovery process is possible, but difficult. |
Finding the Solution with Value Iterations |
| |
The add-in provides an easier way to discover
the states involved in the optimum solution. In the dialog
reached via the Solve button, we set the options as
below.
|
Chose the Value iteration with a fixed
policy (check Fix Policy Box). Near the bottom of the
form, initialize the probabilities to set the probability
of state 1 to the value 1. To see the results, select
the All option,
and Clear the iteration
display by checking the box at the top. The results are
stored on the Well
States worksheet. Click the Hide zero Probs. button
to show only states with nonzero
probabilities.
On clicking OK the add-in evaluates the probability
distribution of the states through the steps of the well
drilling. The process stops when the last two steps have
the same probability. |
|
| |
Part of the worksheet is shown below.
With this option the program sums the state probabilities as
the iterations progress. The sums are in column A. When the process
is complete, all states with zero probabilities are hidden.
The result is a table showing only states that are visited during
the process. The summed probabilities are not a proper distribution
on the state space, because individual states may be visited
several times. For example, the Final state
is encountered several times in the example and it's probability
sum is greater than 1. |
|
| |
The display above shows the state
definitions and the state values and probabilities at termination.
The state probabilities for each
iteration are stored starting in column P. In the figures
below, some columns are hidden for clarity. The initial state
probabilities and the first two iterations are below. Step
0 shows the state values and probabilities after the initial
solution has been imposed, but before any computational iterations.
The probability vectors in columns T, W and Z show the
state probabilities for each step. We see that starting in
state 1, the next step has states 28 and 55 with probabilities
0.47 and 0.53, respectively. The next step moves to states
56 and 57. There is also has a 0.47 probability
that drilling will terminate.
|
|
| |
Steps 4
through 6 are below. The program stops at step 6 because the
results in step 5 and 6 are identical. |
|
| |
Notice that the states visited do
not include well 4. The process always terminates before well
4 is considered. Well 4 is not a viable candidate
under any circumstance. |
| |
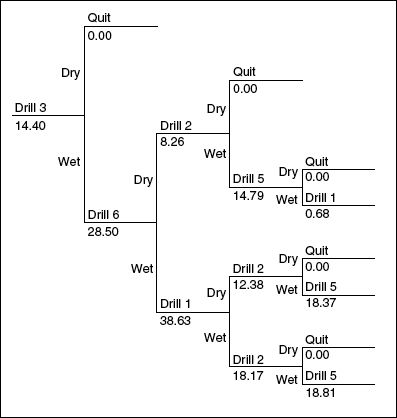 |
The figure shows the decision tree for the
optimum solution. There is sufficient information from the
reported results to construct this tree. (The figure was
borrowed from the paper.) |
|
Conclusion |
| |
This example illustrates that problems with
fairly large state spaces can be modeled and solved with the
DP add-ins. The solutions on this page were each obtained in
about one minute of computation. The example also indicates
an approach to other sequencing problems. The important distinction
in this case is that the transition probabilities depend only
on the set of wells already drilled and not the exact sequence
of drilling. Of course the number of items that can be sequenced
by this approach is small, since each additional item doubles
the number of states. |
| |
|



