|
|
 |
Mathematical
Programming Model
Builder |
 |
-
Formats |
|
The general linear
programming model has a linear objective function, linear constraints
and lower and upper bounds for the variables. The model has n variables
and m constraints. Since the expressions for the objective
function and constraints are linear, the model is completely
described by the coefficients of the objective, the coefficients
of the constraints, bounds for constraints, and lower
and upper bounds for the variables. The formats available with
the MP model builder differ on how this information is stored.
 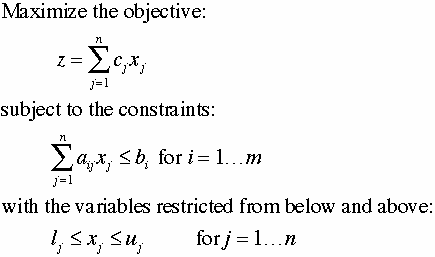
This page shows the model formats available with
this add-in. The add-in only creates math Programming models
for LP and IP. The tableau format is similar to the
LP model created by the Math
Programming add-in. The others are new. The following pages
expand on the different formats. |
Building a Model |
| |
|
To create a new model choose the Linear/Integer command
from the ORMM menu.
The menu has three additional commands. The worksheet
holds buttons to call various add-in procedures. These
buttons are linked to the computer that creates a model,
and a link error is generated when the worksheet is opened
on a different computer. Choose the Add Buttons command
to erase the buttons and create new ones. When you expect
the worksheet to be used on someone else computer, choose
the Remove Buttons command before saving. The About
Add-in gives the release date of the version of the
add-in that you are using. Make sure you are using the latest
release. The latest release date is on the Excel
page for this
add-in. |
|
The Choose Format dialog lists
the
formats are available and provides a field for specifying
the problem name. The name entry is used to provide
Excel names to many ranges on the worksheet. The name must
satisfy Excel's restrictions for naming ranges, that is:
the names must not contain spaces, they must start with
a letter and they may not include punctuation marks. If
an error occurs when this dialog closes, try a different
name for the problem. The program automatically suggests
names like LP_1, LP_2 and so on. The user may prefer a
more descriptive name. Once
it is specified the name cannot be changed.
We choose the Tableau option with the name LP_1. |
|
The LP/IP Model dialog appears after the Choose
Format dialog is dismissed. The dialog accepts the
dimensions of the model as well as data regarding the direction
and measure for the objective, the integer variables, the
Solver selection, and the choice for the Sensitivity
Analysis when
the problem is solved.
The Random Data button fills the model with random
values. The Random Number Seed determines the
values assigned, so the same problem can be assigned to
different formats. The Mac and Windows versions of Excel
give different models for the same seed.
The entry in the Coefficients section indicates
the number of coefficients to be entered. For the tableau
format, coefficients are specified for all rows and columns,
so the number of coefficients is automatically specified
as the product of the number of variables and the number
of constraints.
The checkboxes for upper and lower limits specify whether
vectors are provided to hold these limits. If unspecified,
lower limits are zero and upper limits are large numbers.
Checking the Variable Type box includes an
array that
specifies whether each variable is Real or Integer.
If integer variables are included in the model definition,
this array is included automatically. When checked the Dual
Solution checkbox creates arrays for the dual solution
in both the variables and constraints regions of the worksheet.
All of these entries except the name and the feature choices
can be changed with the Change button after
the worksheet is constructed.
In the examples of this section the figures show
the dual variables associated with the solutions. These results
are interesting from a theoretical viewpoint and often
have relevance in practical problems. For those
interested in only the solution of the linear or integer
model, it is not necessary to view or understand
the dual variables. |
|
Parameters and Buttons |
| |
Dismiss the dialog with an OK
indication and the program builds a worksheet holding one of
the formats described on this page. The formats all place buttons
and parameters at the top of the worksheet. None of the values
in this section are under direct control of the user and they
should not be changed. The upper left
corner holds the model name prefixed with the label "List
Model".
The yellow range in column A shows data used by the Jensen
LP/IP Solver when that solver is active. It can be changed
by selecting the LP/IP Solver item on the ORMM menu. When the
Excel Solver add-in is active, the Excel Solver model is stored
in this range. The range in column F describes model parameters.
Column I holds information controlling the solver. Column L
has solver output results. Column O is constructed when the the
dual solution is displayed on the worksheet.
Cell F4 is important because it holds the objective function
for the model while F3 holds the direction of optimization
(Max or Min). Some of these entries in columns F and I can
be changed by clicking the Change button. |
|
| |
The Change button opens
the model dialog to change the size and other features of the
model. The Solve button
calls the selected solver. The Equation button rewrites
the equations of the model. This is generally unnecessary but
can be used to fix errors.
The Change
Relation button changes constraint relations (<=, >=,
=). It is only effective if the selected range is on one or more
relation cells. |
The Tableau Format |
| |
The formats differ on how the
components of the model are arranged on the worksheet. For
the tableau format the variable information is arranged in
rows at the top of the worksheet. The constraint information
is arranged by columns at the left side of the worksheet. The
constraint coefficients are stored in a matrix lying below
the variables and to the right of the constraints. |
|
| |
The variable data
is arranged by row. Row 10 holds variable names and rows 12
through 15 hold the type, lower bound, upper
bound and objective coefficient terms. Row 11 holds the primal
solution to the problem and is filled by the Jensen LP/IP
Solver add-in or the Excel Solver add-in. We indicate with
the green outlines the cells that are filled in by the solver.
The numbers in rows 16 and 17 are the dual variables
for the lower and upper bounds. In LP theory discussions they
are called the Reduced Costs for the variables. For
maximization problem the reduced costs are negative for variables
at their lower bounds and positive for variables at their upper
bounds. The dual values are computed by the add-in and surrounded
by red outlines.
The constraint information: name, dual values, value, relation
and bound are described in columns E, F, G, H and I respectively.
The dual variables for constraints are usually called the shadow
prices. It
is filled by the Jensen LP/IP Solver add-in. The constraint
data is arranged by columns.
The constraint coefficients are stored in a matrix with rows
representing constraints and columns representing variables.
This is an efficient representation when the constraint matrix
is dense (most coefficients are not equal to zero). In many
practical instances, constraint matrices are sparse where most
coefficients are zero. The sample problem is small, but practical
problems may have many hundreds (or thousands) of variables
and many hundreds of constraints. Although the solution of
very large problems is beyond our add-ins, it is not unlikely
that problems may have a few hundreds
of variables and several dozens of constraints.
Then the matrix format is very inconvenient. The matrix is
a vast expanse on the worksheet and the user may have a tough
time entering and checking the data for even moderately sized
problems.
Older versions of Excel are limited to 256 columns. Since
the variables are arranged by columns, this automatically limits
the model size to about 250 variables. This limitation is not
so great for Excel 2007 and later versions because these allow
many more columns. |
The Dual Tableau Format |
| |
The dual tableau format is the transpose
of the tableau format. Here constraints have the row orientation
while variables have the column orientation. The constraint coefficient
matrix as also transposed. For most problems, the number
of variables is much greater than the number of constraints.
When models are limited to 256
columns, the dual tableau representation is preferred for problems
with more than 250 variables. |
|
| |
It is important to observe that this format represents the primal LP
model and not the dual LP model. It is simply a reorganization
of the primal data. |
The Column List Format |
| |
The list format replaces the constraint
coefficient matrix with a list. This format has the variables
and constraints in arranged in columns. The constraint coefficients
are stored in columns U through AA. Each coefficient has: index,
column number, row number, name, coefficient value, the value
of the variable associated with the column index, and the product
of the coefficient variable and the coefficient value.
Several columns are yellow indicating that they contain formulas.
The coefficient name, column X, is computed using a formula
that combines
column and row names. The coefficient variable, column Z, is
computed by referencing the appropriate cell in the solution,
column J. The coefficient value, column AA, is the product
of the values in column Y and column Z. The numbers in the constraint
value, column Q, are computed by summing the appropriate
entries in column AA. The Excel function SUMIF is used for this
calculation.
The advantage of this format is that it uses a fixed number
of columns, independent of the problem size. The problem size
is reflected in the number of rows used. The number of rows
is very large for the current versions of Excel (more than 1,000,000). |
|
| |
The list format is much more efficient
than the matrix for storing sparse constraint sets. It is unnecessary
to store 0's in the list. This example doesn't illustrate
this efficiency since the number of coefficients is the product
of the numbers of variables and constraints. I expect that programs
that automatically generate the data for the model will take
advantage of the list structure. I plan to create an add-in that
will automatically generate LP data in a manner to the DP
Data add-in.
The current version of the LP/IP solver requires that the
coefficient list be sorted by column order. The sorting is automatically
accomplished when the Solve button is pressed. |
The Row List Format |
| |
The row list format is the transpose
of the column list format. All data is described by rows. The
figure below shows part of the coefficient list since the full
list of 50 columns would be difficult to display. For some problems
the row list format may be convenient. The number of columns
allowed by Excel may limit the use of this format since the number
of nonzero coefficients will always exceed the number of constraints. |
|
| |
|
|



