|
|
 |
Network
Flow Programming |
 |
- Example Problem - Power Distribution |
|
|
Consider a regional power system with three
generating stations: A, B, and C. Each station serves its own
local area. Three outlying areas are also served by the system:
X, Y, and Z. The power demanded at areas X, Y, and Z is 25 MW
(megawatts), 50 MW, and 30 MW, respectively. The maximum generating
capacity beyond local requirements and the cost of generation
at the three stations is shown in the table.
Power can be transmitted between any
pair of generating stations, but 5% of the amount is lost. Power
can be transmitted from some of the generating stations to the
outlying areas, but 10% of the amount is lost. Lines exist from
stations A and C to X, from B and C to Y, and from A and B to
Z. Our goal is find the minimum cost power distribution plan
between generating stations and to outlying areas.
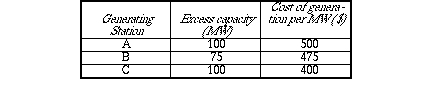
|
| |
The network model for this problem
consists of nodes and arcs as shown in the figure. The nodes
are the circles and represent the generating stations and cities.
The arcs are the directed line segments between nodes. They represent
the transmission lines between generating stations and/or cities. |
| |
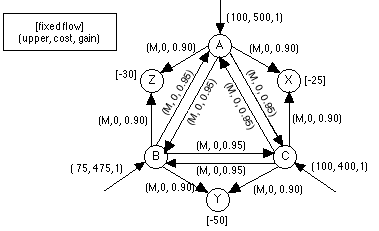
Network Flow Model of Power Distribution Problem
|
| |
The numbers adjacent to the nodes
in the square brackets represent flows entering the network
or flows leaving the network, positive numbers for flows entering
and negative numbers for flows leaving. Power enters at the
generation stations, nodes A, B, and C through arcs that enter
these nodes. Power leaves the network at nodes X, Y, and Z,
where the negative numbers at the nodes indicates the amounts
to be withdrawn at the nodes. The arcs for this case have three
parameters, the upper bound, cost and gain. The upper bound
for each transmission arc is M, indicating a large number.
For an arc that passes from node i to node j,
the gain multiplies the flow leaving node i to obtain
the flow that enters node j. For this problem the gain
factors represent the losses of power in the transmission lines.
A solution to the network model is an assignment of flows
to the arcs that satisfies the flow requirements at the nodes.
Flow is conserved at each node in that the total flow entering
must equal the total flow leaving. An arc that touches only
one node, such as those entering A, B and C, contributes only
to the conservation equation for that node. The optimum solution
minimizes cost. |
| |
|
|



