 |
This page describes additional features of the Functions
portion of the Random Variables add-in. |
Addresses |
| |
Whenever the random variables are
used in worksheet locations other than on the function form, their
values must be linked to those locations with Excel formulas.
Also, when the function values and feasibility states are computed
elsewhere formulas linking to the form must be provided. This
is simplified somewhat by the Address feature of the
add-in. Clicking the Include Address checkboxes to use
this feature. |
| |
|
| |
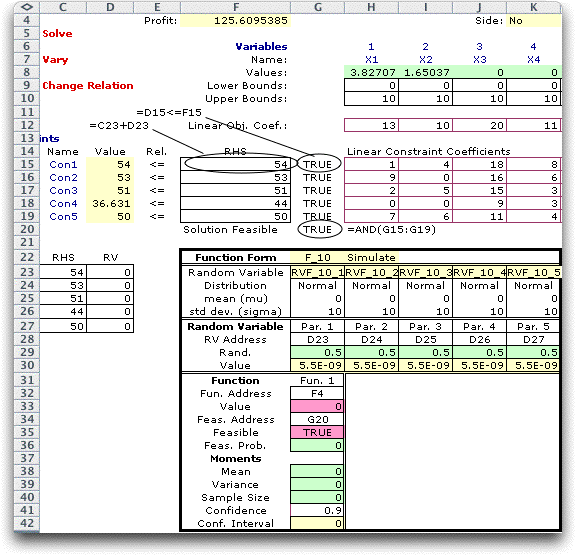
To illustrate, we use another example
from stochastic programming. We consider the same LP as on the
Algorithms page, but here we assume that the decisions
are fixed. The random variables affect the RHS vector and determine
whether this solution is feasible. This is called the No
Recourse decision situation because once the decision is
made there is no further recourse. In the example below we fix
the decisions at the optimum solution of the deterministic problem
(using the expected values of the RHS). We allow the RHS to
deviate according to a Normal distribution with mean 0 and standard
deviation 10. The questions is what is the probability that
the solution is feasible? The worksheet below is modified to
answer this question. The RHS values are the sum of the initial
values and the random deviations. Equations in the range G15:G19
determine whether each constraint is satisfied. The equation
in G20 evaluates as TRUE only when all constraints are satisfied.
We enter on the function form the addresses where the random
variables are to be stored, D23:D27. We enter F4 as the address
of the objective and G20 as the address of the feasibility state. |
| |
|
| |
When the Moments
command begins the simulation, the appropriate formulas
are automatically entered on the worksheet. The new formulas
are shown in red below. This feature removes the requirement
that the analyst provide the formulas. It is particularly useful
if several function forms on the worksheet address the same
model. |
| |
|
| |
The figure above shows the results
of 1000 simulated samples. The function mean is has the same value
as the LP solution and the variance is zero. This is expected
because the solution X1 through X10 is the same for all samples.
The interesting result is in G36. Here we see that only 5% of
the samples were feasible. This is also not surprising since the
solution is feasible only if all the constraints are
satisfied. |
Additional Functions |
| |
It is interesting to repeat the
example with additional functions reporting the values of the
decision variables. A version of the LP model is repeated below.
We identify two cells for special attention. Cell F4 holds the
objective value and cell O5 holds a logical expression that
returns TRUE when the word "Optimal" appears in O4
(when the model is feasible). The cells in row 11 contain logical
formulas. These evaluate as TRUE if the corresponding decision
variable is greater than (1/100) and the solution is feasible.
The expressions identify which variables are non-zero in the
LP solution. |
| |
| |
A function form is shown below using
addresses to identify the random variables, functions and feasibility.
Our purpose with this form is to simulate the RHS vector. For
each sample we will solve the LP and record the objective value
(F4) and decision variable values (H8, I8, ...). This is the Wait
and See Policy described on the Algorithm
page. We specify O5 as the feasibility indicator for the
objective function. The logical expressions in row 11 indicate
when data will be collected for the decision variables. Data will
be compiled only when the cells in row 36 evaluate as TRUE. We
have increased the standard deviation for each Normal distribution
from 10 to 30. This makes infeasible models much more likely. |
|
|
| |
The results show that about 79% of
the samples had feasible, hence optimal, solutions. The average
objective (107.6) is much less than the value (122) obtained with
standard deviation of 10. The feasibility proportion for a decision
variable indicates the proportion of the samples for which that
decision variable was non-zero. We used 1/100 as a limit to eliminate
solutions with very small values. Variables X3, X7 and X9 are
never used for the 1000 samples. Variables X1 and X8 are nonzero
for a majority of the samples. These results might be useful to
an analyst trying to identify the important variables of the model
when the RHS vector is uncertain. |
|
Display |
| |
It is sometimes useful to review the results
of a simulation or enumeration in detail. This option is provided
by the Display feature. To make a display click the
Display Results checkbox. |
| |
|
| |
A table is created to the right of
the function form and as the simulation runs the data for each
sample is placed on the table. The example below shows 20 simulated
values for the problem considered at the top of this page. The
five random variables and function values are shown. If a particular
sample is infeasible, three stars (***) replace the function value.
None were infeasible for the example. When the number of samples
exceeds 1000, only the first 1000 samples are listed. The display
allows additional statistical analysis of the results. Of course,
creating the display takes time and memory. |
| |
|
Step Program |
| |
To show each sample of an enumeration
or simulation click the Step Program checkbox. This is
especially useful to debug a model. |
| |
|
| |
At each step the sample is placed
on the worksheet and the function values are computed. A dialog
asks whether to stop the step process. An example is below. The
current value of the random variables, function values and feasibility
states are shown. Once the step process is terminated, the sampling
continues. The statistics are computed when the sampling is complete. |
| |
|
| |
The Function feature of
the Random Variables add-in can be used for many applications
in operations research as well as for general use in all kinds
of spreadsheet analyses. |
| |
|



