 |
The examples given to this point are dynamic. After the values
of the random variables are changed, the expressions computing
the function values and feasibility states are automatically evaluated.
The add-in controls when the worksheet is recalculated, but the
Excel program manages the details of the calculation. Some OR
models, such as mathematical programming, require algorithms to
determine values. Unless the algorithms are implemented in user-defined
functions, the cells holding the results of algorithms are not
dynamic. A button on the worksheet or a command on a menu must
be clicked to initiate the algorithm. The add-in implementing
the algorithm places the algorithm results on the worksheet.
There are many cases when we would like the enumeration or
simulation to include the results of an algorithm. An example
is a mathematical program where uncertain parameters are modeled
as random variables. One assumption in this context is that
the decision maker can wait to make a decision until after the
random variables are realized and then determine the optimum
solution. Say we would like to learn about the distribution
of the optimum objective value. This could be accomplished with
the Functions feature of this add-in if the solution
algorithm could be called for each sample of the random variables.
This capability is provided by the Algorithm feature.
On this page we provide a general discussion on the use of the
algorithm feature. We provide complete examples elsewhere.
|
An LP Example |
| |
To illustrate the Algorithm
feature we use the LP model below. The model was constructed using
the Random Problem option of the Math Programming
add-in. The solution shown is optimal. We consider a situation
where the right-hand-side values in the range F15:F19 are random
variables. We assume that the decision maker can wait to choose
values of the variables X1 through X10 until after the RHS values
are known. Our problem is to learn about the distribution of the
optimum objective value. |
|
| |
The model of the stochastic features
is constructed by choosing the Add Function command.
The dialog below is presented. We have selected the simulation
option. During the simulation process, the add-in will run the
specified algorithm at every evaluation of a sample if a valid
algorithm is named in the Algorithm field. For the
current example we enter LP/IP. This indicates that for every
sample, the solution of the LP will be computed with the Jensen
LP/IP add-in. |
| |
|
| |
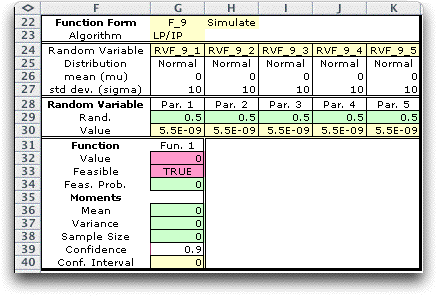
The function form is placed on the
worksheet below the LP model. An additional row is added just
below the title (row 23). The name of the algorithm is in G23.
Some algorithms require additional parameters. These are placed
to the right of the name starting in cell H23. |
| |
|
| |
The example will call the Jensen
LP/IP Solver at each sample point. In order to use that algorithm,
a linear programming model constructed with the Math
Programming add-in must be present on the worksheet and the
LP/IP add-in must be installed. |
Linking the Models |
| |
Before proceeding, the LP form
must be linked to the Function form. We have chosen the random
variables to represent deviations of the RHS values from the
original values. Two kinds of links are required. The random
variables of the Function form must be linked to the input cells
of the LP model, and the LP solution and its feasibility must
be linked to the function values of the Function Form.
These are illustrated below.
The random variables are in row 30. These are linked to the
RHS values with an Excel function. We find in cell F15 the function,
=C23 + G30.
Similarly the other RHS values are linked to the
random variables. The example shows the effect.
The LP objective is in cell F4. We link that to
the function form by placing in G32 the equation:
=LP1_Obj.
This is the name of F4. The feasibility state
equation is in G33 (not shown). That equation returns TRUE when
the LP has a feasible solution and FALSE when it does not. |
| |
|
Simulation |
| |
To perform the simulation we choose
Moments from the menu. The results of 1000 simulation
iterations are below. All simulated samples were feasible and
the mean simulated objective (122) is less than the deterministic
objective value (125.6). We consider this example further on the
Stochastic Programming pages. |
| |
|
Named Algorithms |
| |
We have used math programming
as an example, but the algorithm feature can be used for a variety
of situations. Several named algorithms are available, and the
user can provide references to others. The named algorithms
and their conditions for use are listed in the table. Links
on the names lead to more detailed descriptions.
| Algorithm Name |
Purpose |
Condition for Use |
| LP/IP |
Solve an LP |
The LP/IP add-in must be installed and the active worksheet
must contain an LP model constructed by the Math Programming
add-in. |
| Network |
Solve a Network Model |
The Jensen Network Solver add-in must be installed and
either a network model or a transportation model constructed
by the Math Programming add-in must be on the active worksheet. |
| Solve_MP |
Use the Solver specified for the MP model |
The Math Programming add-in and whatever add-in used for
the solver must be installed. This command can call the
Excel Solver for nonlinear models. |
| IRR |
Compute the Internal Rate of Return |
A NPW model constructed by the Economics add-in must be
on the active worksheet. The Economics add-in must be installed.
This algorithm also needs the name of the model. The name
of the model is placed in the cell to the right of the name
"IRR". |
The call statement for the algorithms are programmed
in VBA using a command similar to the one below.
my_result = Application.Run("lpip_solver.xla!Solvmod")
By placing the name of the subroutine in this format
in the Algorithm field, any algorithm programmed in
VBA can be run. For example if the string below is entered,
the LP/IP solver will run with each simulation. The add-in name
is first, then "!" and then the subroutine name.
lpip_solver.xla!Solvmod
We illustrate each of the named cases on the pages
elsewhere on this site. |
| |

|



