The solution to the problem of
modeling the nonconcave profit functions is to add binary (taking
the values 0 and 1) variables to the model. The
new variables control the order that the pieces of the profit
function are used in the solution. For product Q we need two
new variables and modify the bound constraints for product
Q as below.
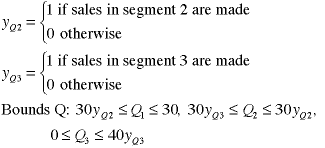
From the bounds we see that if 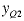 is
0, only is
0, only 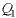 is
allowed to be greater than 0. If is
allowed to be greater than 0. If 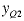 is
1 and is
1 and 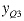 is
0, is
0, 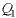 is
forced to 30 and is
forced to 30 and 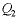 is
allowed to increase. If both is
allowed to increase. If both 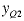 and and 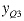 are
1, are
1, 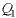 is
forced to 30 and is
forced to 30 and 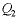 is
forced to 30 and is
forced to 30 and 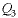 is
allowed to increase. is
allowed to increase.
The variables representing R are controlled
by a single binary variable. The variable and revised bounds
are shown below.
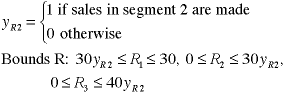
Only one variable is necessary because there
is only one convex portion of the profit function. The complete
Excel model with the optimum solution is illustrated below. |

