To begin creating a model, variables
must be defined to represent each decision. In many cases models
can be more succinctly stated using algebraic expressions with
subscripted variables. In this section, we use variable names
like A1, A2, … C3, and C4 to represent the decisions.
This makes it easier to present the model in a browser readable
format. The notation is also similar to that used for the computer
model. We will write several models in this section, but the
simplest is:
Objective: Max. z = 6*A1 + 7*A2 + 9*A3 ...
+ 19*C3 + 20*C4
subject to:
Budget: 13*A1 + 20*A2 + 24*A3 ... + 48*C3 +
55*C4 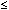 100 100
Simple Bounds and Integrality
0 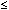 A1 A1 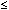 1,
0 1,
0 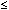 A2 A2 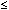 1,
... , 0 1,
... , 0 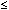 C4 C4 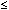 1
and integer 1
and integer
We use * to indicate multiplication and ... to
indicate a continuation in a similar fashion.
Note that since the variables are restricted
between 0 and 1 and required to be integer, there are actually
only two feasible values, 0 and 1 for each variable. A design/location
combination either adds its contributions to the net income
and budget (=1) or does not (=0). The simple phrase "and
integer" specifies that all the variables must be integer
Thus the model describes the problem of selecting the set of
design/location combinations that maximize net income, while
not exceeding the budget constraint.
The model has the linear form required for linear
programming, but it is not a linear programming model because
the variables are not allowed to assume all values within a
continuum. Often the phrase Integer Programming is used
for the linear model with some or all the variables required
to be integer, leaving out the term linear. Although one can
express models that are integer and nonlinear, these are generally
much more difficult to solve. For a nonlinear-integer model
we use the phrase nonlinear-integer program. We only consider
(linear) integer programming models in this section. |