In the following we create a model with the Math Programming add-in and solve it with the Jensen LP/IP solver add-in. We first solve the model when the integrality condition is dropped, thus obtaining a linear program (LP). This is a common practice for very large models, because the linear program is much easier to solve that the integer program (IP). We do it here to illustrate some general relationships between the LP and the IP solution. The LP solution is shown on the worksheet below. The solution has

z = 40.9, A1 = 1, B3 = 1, B4 = 1, C1 = 1, C3 = 0.52.

The solution uses the entire budget.

The LP model is called a relaxation of the IP model, because one of the restrictions of the IP model has been removed. One might be tempted to round the LP solution to obtain an integer solution. In this case rounding C3 up to 1 gives an infeasible solution because it violates the budget constraint. Rounding C3 down to 0 gives a feasible solution, but it is not optimal for the IP. In general, rounding noninteger optimal LP solutions to integer ones will not provide the optimum IP solution. In more complicated problems it is often difficult to find a feasible solution by rounding.

We observe from the solution that although integrality was not required, all the variables but one have integer values. This is because the optimum LP solution is a basic solution, and a basic solution has as many basic variables as there are constraints. Every nonbasic variable is at either its upper bound (1) or lower bound (0), while nonbasic variables may assume fractional values. With only one constraint, one would expect no more than one fractional value as we see here. It is possible that a basic variable will assume one of its bounds. Such a solution is called a degenerate solution. For degenerate solutions, the number of values not equal to 0 or 1 will be less than the number of constraints.

We note at the top of the Excel display that finding the LP solution with the Jensen LP/IP solver required only 3 iterations of the simplex method. Although the time indication is 0, it is actually less than 1 second, the smallest number the time field can display.

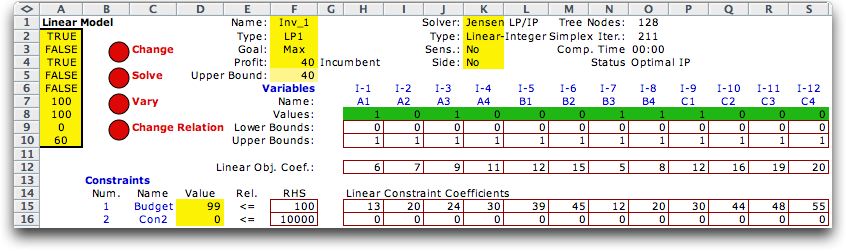
We change the LP model into the IP model by re-imposing integrality. The Excel model indicates this by prefacing the index of each integer variable by the letter I. If only a subset of the variables were required to be integer, only the ones in the subset would have the I-preface. The solution as shown below has the values:

z = 40, A1 = 1, A3 = 1, B3 = 1, B4 = 1, C1 = 1.

Comparing this solution to that of the LP, we see that A3 has replaced C3 in the decision set, with A3 having the value 1. The objective value has decreased to 40. It will always be true that the optimal IP objective value is no greater than the optimal LP objective value, because the IP feasible region is more restrictive than the LP feasible region. Because of the discrete nature of the solution, the budget is not entirely used.

We also see that the IP solution takes much more computational effort than the LP solution, requiring 132 simplex iterations, compared to the 3 necessary to find the LP optimum. Although the time required is only 1 second, this is an indication that IP solutions will be much harder to come by than for the solution for the LP model. Since the LP solution is guaranteed to be at an extreme point of the feasible region (a basic solution), we only need to consider 3 of these to find the solution. The integer solution is usually not an extreme point, so a complicated search process is necessary to locate it. The 70 tree nodes shown above the time requirement is a measure of the difficulty of this search. Compared to the 70 tree nodes explored there is a much larger number of possible solutions to the model. Considering all possible assignments of 0 or 1 to the 12 variables, there are, in fact, 2 raised to the 12th power integer solutions to this problem, 2096 solutions. Refer to the IP Methods section of this site for more discussion about the procedures for integer programming.