Selecting the Markov Chain (DTMC) item on the Markov Analysis menu creates the DTMC model. Two sheets are constructed, the Matrix worksheet and the Economics worksheet. The data from the Model worksheet is automatically transferred to the two new worksheets. The Matrix worksheet is shown below. In column G we see an analysis of the current transition matrix. It has one class of recurrent states. The analysis cannot determine whether the matrix is cyclic.

Cells are colored to indicate the source of their contents. Cells outlined in maroon hold user data. Although the data here was transferred from the Model worksheet it can be changed by the user. Cells colored yellow hold formulas created by the add-in. They should not be changed. Cells colored green are filled by the computer.

The Change button allows the user to change the dimensions of the matrix. The Calculate button calculates all formulas in the event the Manual calculation option has been chosen for the worksheet. The Analyze button performs the state-class analysis. If the transition probabilities in the matrix are changed the state-class analysis must be performed before other analyses can take place.

Buttons arrayed along the left margin perform the analyses indicated. In each case, clicking a button creates a new worksheet of the type required by the analysis.

Economics

Transient Analysis

The transient analysis computes the probability distribution of the state starting from a specified initial state. In the example below the system starts with 0 failures on the first day. After one day the state probabilities are as shown in the row labeled 1. The display shows the probabilities for 20 days or steps. For this example, the probability vector approaches the steady-state values after only a few days of the process. Clicking the More button gives 20 additional days. The Start button allows a different selection of the initial state.

The program shows the expected values of the step cost, cumulative cost and discounted cost for each step.

Steady-State Analysis

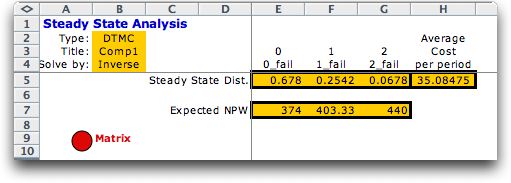
For DTMC's with only a single class of recurrent states, a steady-state probability vector can be computed. For acyclic systems, the transient probabilities converge to the steady-state probabilities as the number of periods grows. The steady state probability for state j is the limiting probability that the process is in state j after a large number of steps. It also equals the long-run proportion of time that the process will be in state j.

The analysis also provides the expected value (average) or the per-period cost at steady-state.

n-Step Probabilities

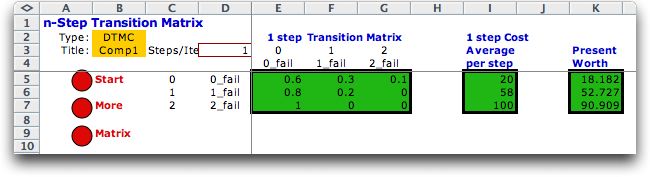
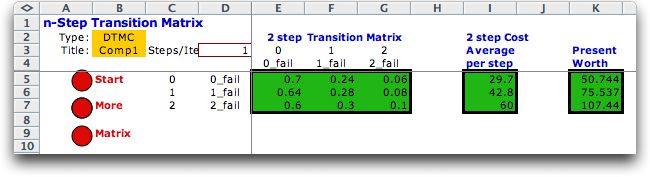
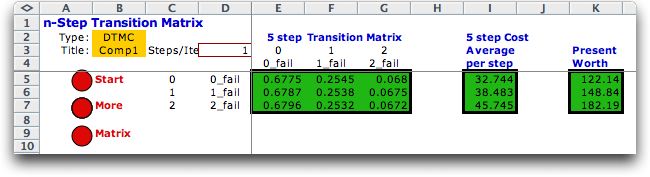
This analysis computes a matrix showing the probability of going from state i to state j in n steps for all pairs of states. The 1-step probability matrix is just the transition matrix as shown below. By clicking the More button the step number is advanced to 2 and the matrix holds the 2-step probabilities as shown in the second illustration. The third case shows the 5-step matrix. The rows of the matrix have become very similar and are all approaching the steady-state vector. Average step costs and present worth values are also shown.

First Pass

Given some initial state it is sometimes interesting to compute the probability distribution for the number of steps (days) required to reach some other state. The first pass analysis provides this for any two states. The example below shows the analysis for the number of days required to pass from state 0 (no failures) to state 2 (2 failures) for the first time. The probabilities are shown in the column labeled PF(i, j, n). Note that this is accomplished in 1 step with probability 0.1, the probability of both computers failing during a single day. For n > 1, a complex series of events must occur for the passage to occur for the first time. At the bottom of the list we see the sum for the first 20 days (0.776). This is the probability that the first passage occurs in 20 days or less. Clicking the More button, provides the probabilities for days 21 through 40. The button can be pressed repeatedly to get the analysis for any number of days.

The analysis also provides the expected number of steps required to pass for the first time from each state to the to state of the analysis (state 2) in this case. These results start in cell J5. The expected value for first passage from state 0 to state 2 is 13.75 days.

Simulation

Absorbing State Analysis

An absorbing state is a state that traps the process. Once the process enters an absorbing state it never leaves. The example considered at this point does not have an absorbing state, so we change the situation in the following manner.

To model this situation we introduce two new states, Sell and Buy New. The number of states is easily changed by clicking the Change button on the worksheet and entering the new number of states (5). The new matrix adjusted for the situation is shown below. The two states are absorbing states as indicated with the transition probabilities of 1 on the diagonal of the matrix. The matrix analysis shows that the two new states are recurrent states. Once entered, the process never leaves these two states. The original states are transient states in that there is a nonzero probability that once the process leaves one of these states that it will never return.

Eventually the system will enter one of the absorbing states. The question is which will it enter? This answer can only be given by probabilities because the transitions that occur are random. The answer also depends on the state in which the process begins.

The absorbing state analysis on the worksheet shown below provides useful information. It is apparent that whatever the initial state there is about a 0.9 probability that the office manager will eventually sell the computers and only a 0.1 chance that he will buy perfect ones. If the system begins with two failures the chance of buying perfect computers is slightly higher.