Time

State

The state describes the situation at a point in time. Because the states are required to be discrete they can be identified with nonnegative integers 0, 1, 2, 3... and so on. There may be a finite or an infinite number of states. For this introductory discussion, it is easier to concentrate on the finite case and use m - 1 as the maximum state index. The sequence of random variables

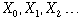
is the stochastic process that describes the state at time t. Each 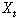can take one of m values.

Depending on the situation, the state may be very complex or very simple. We use a v-dimensional vector of state variables to define the state.

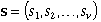
In constructing a model, it must be made clear what the one-to-one relationships are between the possible state vectors and the nonnegative integers used to identify a state in a DTMC. We call the state associated with index i, 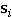. Depending on the context, i typically ranges from 0 to m - 1 or from 1 to m. The state definition must encompass all possible states; however, the system can reside in only one state at any given time.

The computer repair example allows a simple state definition with only one component, s = (n), where n is the number of computers that have failed when the system is observed in the morning. Note that the system is observed after the repaired units are delivered but before any failures occur. The list of possible states for the example appears in Table 1. The value of m is 3. In this case, the state index is conveniently identical to the variable defining the state; however, this relationship will not always be true. We assign a cost of operating the system for one day that depends on how many computers are failed. The cost is $50 per computer failed. This cost is a function of the state.

Table 1. States for the example
Index	s	State definitions	Cost
0		No computers have failed. The office starts the day with both computers functioning properly.	0
1		One computer has failed. The office starts the day with one working computer and the other in the shop until the next morning.	50
2		Both computers have failed. All work must be sent out for the day.	100

Events

To understand the behavior of a DTMC, it is necessary to identify the events that might occur during a single time period and to describe their probabilities of occurrence. Generally, the set of possible events and their probabilities depend on the state s.

Given some current state at the beginning of a period and one or more events occurring during the period, the system will be in some new (next) state at the beginning of the next period. This occurrence is called a transition. One or more events may occur within the period, and by observing them, we must identify the resulting new state at the beginning of the next period.

For the computer example we list the current states in Table 2 together with the set of possible events that might occur during the day. Given the current state and the problem description, one must be able to determine the probability of every possible transition for the upcoming period. We use colored bands to distinguish the states. Note that each state has one or more associated events and that the sum of the probabilities for each state must equal 1. The cost column represents the repair cost of the computers assummed to be $40 per computer repaired.

Table 2. Events, probabilities and transitions
Index	s	Events	Probability	Next state	Cost
0		Neither computer fails.	0.6	(0)	0
		One computer fails.	0.3	(1)	40
		Both computers fail.	0.1	(2)	80
1		The remaining computer does not fail and the other is returned.	0.8	(0)	0
		The remaining computer fails and the other is returned.	0.2	(1)	40
2		Both computers have failed. No failures can occur.	1.0	(0)	0

State-Transition Matrix

The major properties of a DTMC model can be described with the m x m state-transition matrix P whose rows and columns are labeled 0 through m - 1. An element of the matrix, 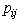, is the probability that given the system is in state i at some time t, the system will be in state j at time t + 1. A requirement of a DTMC is that the transition probability depends only on the current state i and not on the particular path that the process takes to reach state i.

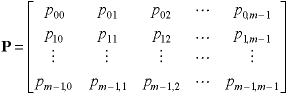
The transition matrix for the computer example is easily constructed from the data in Table 2. The state indices are shown to the right and above the matrix.

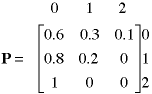
Some general characteristics of the transition matrix are as follows.

• The elements of a row must sum to 1. This follows from the logical requirement that the states define every possible condition for the system.
• All elements are between 0 and 1. This follows from the definition of probability.

State-Transition Network

The information in the transition matrix can also be displayed in a directed network which has a node for each state and an arc passing from state i to state j if 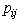is nonzero. The figure depicts the network for the computer repair example. Transition probabilities are adjacent to the arcs. A requirement is that the sum of all probabilities leaving a node must be 1.

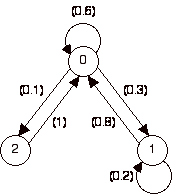
Complete Model

A DTMC model requires the specification of the following.

1. The times when the system is to be observed.
2. The discrete states in which the system may be found. The list of states must be exhaustive. In addition, a one-to-one correspondence must be prescribed between the states and the nonnegative integers.
3. The state-transition matrix showing the transition probabilities in one time interval. Transition probabilities must satisfy the Markovian property, and every row must sum to one.

Although the model structure is easily stated it is not always easy to realize. For example, one might propose time and state definitions (parts (1) and (2) above) for which the Markovian property is not satisfied. This may sometimes be remedied by a more complex state definition.

Because a DTMC model is very general it can be used to describe many interesting stochastic systems. In many cases, however, the number of states required to adequately define the model is very large. As with dynamic programming, this "curse of dimensionality" frequently arises when we try to identify all possible states of the system.