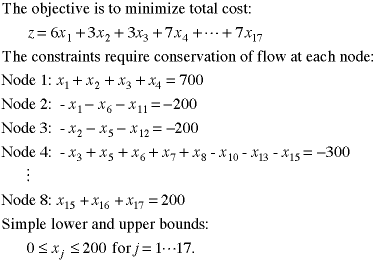Every network flow model has a linear programming model, that is a model with algebraic linear expressions describing the objective function and constraints. We explain here the model for the specific case above, and will provide in the Vocabulary Section, the general model.

For construction of the model, it is convenient to number the nodes and arcs for reference as in Fig. 2.

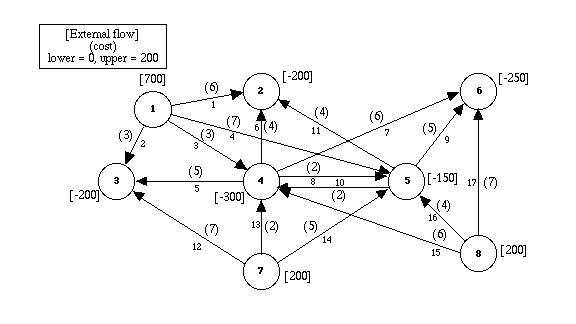
Figure 2. Representation for Linear Programming Model.

The linear programming model is an algebraic description of the objective to be minimized and the constraints to be satisfied by the variables. The variables are the flows in each arc designated by x1 through x17. The network flow problem is to minimize total cost while satisfying conservation of flow at each node. The variables must also satisfy the simple upper and lower bounds on arc flow.