NODES AND ARCS
|
The network flow model consists of nodes and arcs. In the
context of modeling a problem, each node, shown as a circle,
represents some aspect of the problem such as a physical
location, an individual worker, or a point in time. For
modeling purposes it is often convenient to assign names
to the nodes. Arcs are directed line segments. The nodes
at its ends identify an arc. The arc passes from its origin
node to its terminal node. We use m as the number
of nodes and n as the number of arcs. |
ARC FLOW |
Flow is associated with the network, entering and leaving
at the nodes and passing through the arcs. The flow in arc
k is 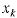 .
Flow is conserved at the nodes, implying that the total
flow entering a node must equal the total flow leaving the
node. The arc flows are the decision variables for the network
flow programming model. .
Flow is conserved at the nodes, implying that the total
flow entering a node must equal the total flow leaving the
node. The arc flows are the decision variables for the network
flow programming model. |
UPPER AND LOWER BOUNDS ON FLOW |
Flow is limited in an arc by the lower and upper bounds
on flow. Sometimes the term capacity refers to the upper
bound on flow. We use 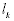 and and
 for
the lower and upper bounds of arc k. for
the lower and upper bounds of arc k. |
COST |
The criterion for optimality is cost. Associated with each
arc k, is the cost per unit of flow, 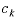 .
Negative values of .
Negative values of 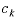 model revenues.
model revenues. |
GAIN |
The arc gain, 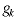 ,
multiplies the flow at the beginning of the arc to obtain
the flow at the end of the arc. When a flow ,
multiplies the flow at the beginning of the arc to obtain
the flow at the end of the arc. When a flow 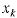 is assigned to an arc, this flow leaves the origin node
of the arc. The flow entering the terminal node of the
arc is
is assigned to an arc, this flow leaves the origin node
of the arc. The flow entering the terminal node of the
arc is
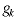 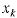 . .
The arc lower bound, upper bound, and cost all refer
to the flow at the beginning of the arc. Gains less than
1 model losses such as evaporation or spoilage. Gains
greater than 1 model growth in flow.
A network in which all arcs have unit gains is called
a pure network. The optimum solution for a pure network
with integer parameters always has integer flows. If some
gains have values other than 1 the network is a generalized
network, and the solution is not usually all integer.
|
ARC PARAMETERS |
The set of arc parameters are shown adjacent to arcs enclosed
in parenthesis:
(lower bound, upper bound, cost, gain).
When a parameter is not shown, it assumes
its default value. Default values are: 0 for lower bound,
infinity for upper bound, 0 for cost and 1 for gain.
|
EXTERNAL FLOWS |
The external flow at node i, 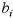 ,
is the flow that must enter or leave node i. A positive
external flow enters the node, and a negative external flow
leaves the node. We show the external flow adjacent to the
node with square brackets. ,
is the flow that must enter or leave node i. A positive
external flow enters the node, and a negative external flow
leaves the node. We show the external flow adjacent to the
node with square brackets. |
FEASIBLE FLOW |
A feasible flow is an assignment of flow to the arcs that
satisfies conservation of flow for each node and the bounds
on flow
for each
arc. |
SIDE CONSTRAINTS |
Side constraints are constraints on arc flows that cannot
be modeled using the network structure, arc parameters
or
external
flows. |
OPTIMAL FLOW |
The feasible flow that minimizes total arc cost is the
optimal flow. |
THE LINEAR PROGRAMMING MODEL |
Every network flow programming model has an equivalent linear
programming model. |

