Critical path analysis is performed by solving a simple set of equations. The purpose is to find bounds on the start and finish time of each activity. Here we use the activity-on-node model, and in the following we use the term node rather than activity. The equations assume that the nodes are indexed in precedence order. That is, the index of each node is greater than any of its predecessors. The equations use the notation below.

On the remainder of this page we derive and illustrate the equations used for critical path analysis.

Early Start

The early start time for a node is based on the logical requirement that a node can begin only when all its predecessors have been completed.

Early Start Time = Latest(Finish Time for all predecessors)

When we assume all predecessors finish as early as possible then:

Early Start Time = Latest(Early Finish Time for all predecessors)

Early Start Time = Max(Early Finish Time for all predecessors)

The early finish time is the early start time plus the activity time for the node.

We describe these relationships with mathematical notation below. The project starts at time 0. The due date is T.

We compute the earliest start times and latest finish times by first setting the earliest start node time for the Start node to 0 and then solving the ES and EF equations for each node in order of increasing node index. It is possible to compute the earliest start time for a node because the earliest finish times for all predecessor nodes have already been computed. The earliest finish time for the End node is the earliest finish time for the project. That must be no more than the due date.

We illustrate the formulas using columns from the project worksheet. We have hidden the columns that are not directly relevant to this calculation. Recall that nodes that have no predecessors shown on the table are immediately preceded by the Start node. Nodes that have no successors shown in the table are immediate predecessors to the End node.

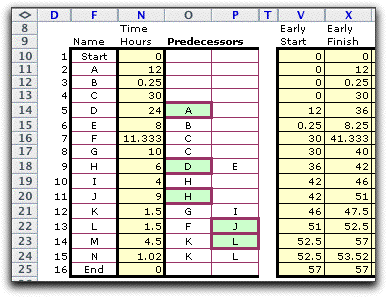
Some of the steps of the process are shown in the table. Nodes 9 and 16 involve two predecessors. Except for the start node, the others have only one.

Node	Name
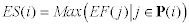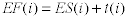1	Start	ES(1)=0	EF(1)=ES(1)+t(1)=0
2	A	ES(2)=EF(1)=0	EF(2)=ES(2)+t(2)=12
3	B	ES(3)=EF(1)=0	EF(3)=ES(3)+t(3)=0.25
4	C	ES(4)=EF(1)=0	EF(4)=ES(4)+t(4)=30
5	D	ES(5)=EF(2)=12	EF(5)=ES(5)+t(5)=36
6	E	ES(6)=EF(3)=0.25	EF(6)=ES(6)+t(6)=8.25
7	F	ES(7)=EF(4)=30	EF(7)=ES(7)+t(7)=41.333
8	G	ES(8)=EF(4)=30	EF(8)=ES(8)+t(8)=40
9	H	ES(9)=Max(EF(5),EF(6)) ES(9)=Max(36,8.25)=36	EF(9)=ES(9)+t(9)=42
...	...
16	End	ES(16)=Max(EF(14),EF(15)) ES(16)=Max(57,53.52)=57	EF(16)=ES(16)+t(16)=57

Latest Finish

The latest finish time for a node is based on the logical requirement that a node must end before any of its successors may be begin.

Latest Finish Time = Earliest(Start Time for all successors)

When we assume all successors start as late as possible then:

Latest Finish Time = Earliest(Latest Start Time for all successors)

Latest Finish Time = Min(Latest Start Time for all successors)

The latest start time is simply the latest finish time less the activity time for the node.

We describe these relationships with mathematical notation below.

The latest finish times and latest start times are computed in the reverse order of the node indices. First we set the latest finish time for the End node to the due time for the project. This must be no less than the earliest finish time for the project. The latest finish time for a node must be the minimum of all the latest start times of all successor nodes. We can compute the latest finish time for a node because the latest start times for all successor nodes have already been computed. We illustrate the formulas using columns from the project worksheet. We have hidden the columns that are not directly relevant to this calculation. Recall that although the form does not show it, the End node has as predecessors all nodes with no successors. In the example, the predecessors of the End node are M and N. For the example, the due date is the same as the early finish time, that is 57.

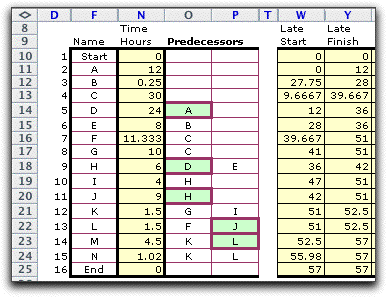
Some of the steps of the process are shown in the table.

Node	Name
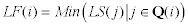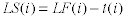16	End	LF(16)=57	LS(16)=LF(16)-t(16)=57
15	N	LF(15)=LS(16)=57	LS(15)=LF(15)-t(15)=55.98
14	M	LF(14)=LS(16)=57	LS(14)=LF(14)-t(14)=52.5
13	L	LF(13)=Min(LS(14),LS(15)) LF(13)=Min(55.98,52.5)=52.5	LS(13)=LF(13)- t(13)=51
12	K	LF(12)=Min(LS(14),LS(15)) LF(12)=Min(55.98,52.5)=52.5	LS(12)=LF(12)- t(12)=51
11	J	LF(11)=LS(13)=51	LS(11)=LF(11)- t(11)=42
...	...
1	Start	LF(1)=Min(LS(2),LS(3),LS(4)) LF(16)=Min(0,27.75,9.67)=0	LS(1)=LF(1)- t(1)=9

Slack Time

The slack time is the difference between late and early start times.

The figure below shows the results shown previously and column AA that computes the slack time for each node.

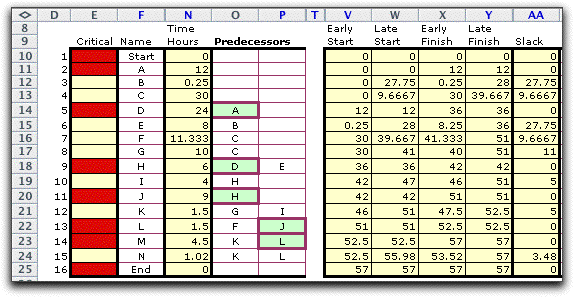
The slack value is the increase the amount of time an activity can be delayed without delaying the completion of the project. When the early start time and late start time are equal, the activity cannot be delayed, so this activity is said to be critical. Activities with positive slack are not critical because they can be delayed without affecting the project duration.

Column E shows the critical activity with a red field, while non-critical activities have a yellow field. If the due date were increased all the slack values would be increased by the same amount. The example below shows the same table with the due date set to 59.

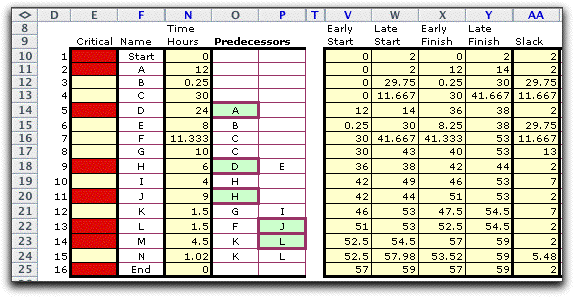
Strictly speaking, none of the activities are now critical with respect to the due date, because the minimum slack value is 2. We define however a critical activity as one that cannot be delayed without exceeding the earliest completion time. With respect to the table, the critical activities are those that have the minimum value of the slack times. The set shown in column E is the same as when the due date is 57.

Analysis with Excel Functions

Here we consider the computation for early and late start and finish times entirely with Excel formulas. This allows an immediate update of the results when an activity time is changed. This method is used for the Project Management add-in. The process is not obvious because the formulas are recursive equations. Obvious attempts to represent the equations with Excel result in circular references. We explain the computations with reference to the worksheet below. The difficulties come when constructing the equations for ES in column V and LF in column Y.

In column V the add-in constructs explicit references to predecessors. A formula computing the earliest start time for a node, solves for the earliest start time by computing the maximum of the earliest finish times of the predecessor nodes. For example the formula in cell V18 computing the earliest start time of node 9 is:

=MAX(X14,X15)

Cells X14 and X15 hold the earliest finish time of nodes 5 and 6. These are the immediate predecessors of node 9. The add-in constructs these formulas from the activity data. Further the early finish times are computed from the early start times. For example the early finish time for node 9 in X18 is computed as:

=V18+N18

Similarly formulas are constructed for the other cells in columns V and X. Although column X depends on column V and column V depends on column X, the formulas do not result in a circular reference because the project network has no cycles. No cell value depends on itself.

Similar formulas are used to calculate the late finish times in column Y. For example the cell Y18 holds the late finish time for node 9. It is computed with the formula:

=MIN(W19,W20)

The latest start time for node 9 is the minimum of the latest start times for immedediate successors of node 9, nodes 10 and 11. Entries in row W depend on row Y. For example, cell W18 is computed with the formula:

=Y18-N18

Again, although column Y depends on column W, and column W depends on column Y, the formulas do not result in circular references because the project network has no cycles. No cell value depends on itself.

Since references to successor and predecessor nodes are explicit on the worksheet, the formulas are no longer valid after changes to the numbers of activities or the precedence relationships.

Critical path analysis provides only bounds on the starting and ending completion times. More detailed schedules are developed when delays are included as described on the next page.