|
|
|
|
Project
Management
|

|
-
Delays |
| |
 |
Critical
path analysis provides only two specific schedules, the early
schedule and the late schedule. For the early schedule each
activity starts at the early start time determined
by the analysis. For the late schedule, each activity starts
at the late start time.
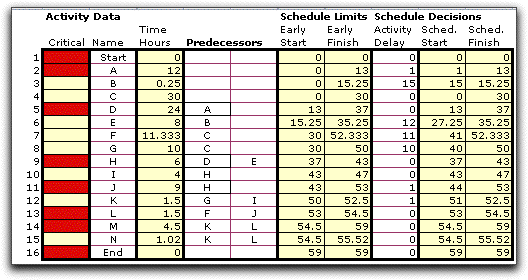
The early schedule is shown below. The early start through
the late finish columns are calculated with critical path
analysis. The scheduled start and scheduled finish
columns provide the start and finish times associated with
a specific schedule. The early start and the scheduled
start columns are the same indicating that each activity
starts at its earliest possible time. The activities with the
minimum slack values are critical. They are marked with the
red bars in the critical column. |
|
| |
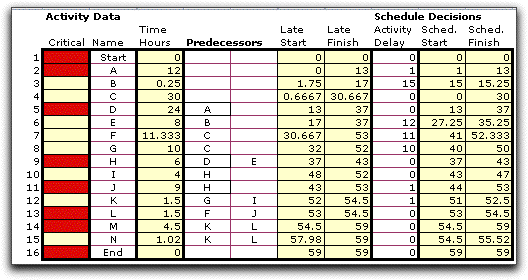
The late schedule is shown
below. The scheduled finish column is the same as the
late finish column. Each activity finishes at its latest
possible time in order to complete the project by its due time
(59). Review of the critical column shows that every
activity is critical. When an activity finishes at the latest
possible time, any increase in the activity time will cause the
project duration to increase beyond the due time. |
|
Activity Delay |
| |
To provide schedules
different than the early and late schedules we define activity
planned delay as the difference between the scheduled
start time and the earliest start time for the activity. To
simplify the discussion we use delay to refer to planned
delay. Again we use node as synonym for activity in the following.
Although we use the same notation for early and late times
as for critical path analysis, we use different equations to
compute these quantities as shown below. In addition to its
usefulness for defining schedules the planned delay for an activity
has relevance for practical planning. |
Early Start |
 |
The early start time
for a node is the time when all its predecessors have finished.
Early Start Time = Max(Early Finish
Time for all predecessors)
Including delay, the formulas for early start,
early finish, scheduled start and scheduled finish times are
below. We include a delay for node 1 representing a delay in
the start of the project. The finish time for node n,
the end node, must be less than or equal to the due time.
We evaluate these formulas in order of increasing node index.
We illustrate the formulas using columns from the project worksheet.
We show only columns that are directly relevant to this calculation.
Recall that nodes that have no predecessors shown on the table
are immediately preceded by the Start node. Nodes that
have no successors shown in the table are immediate predecessors
to the End node. The due time is 59 in this analysis.
We have arbitrarily specified delay for some of the activities.
Some of the steps of the process of solving the
equations are shown in the table. Of the nodes shown, nodes
9 and 16 involve two predecessors. Except for the start node,
the others have only one.
Node |
Name |
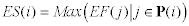 |
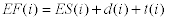 |
1 |
Start |
ES(1)=0 |
EF(1)=ES(1)+d(1)+t(1)=0 |
2 |
A |
ES(2)=EF(1)=0 |
EF(2)=ES(2)+d(2)+t(2)
EF(2)=0+1+12=13
|
3 |
B |
ES(3)=EF(1)=0 |
EF(3)=ES(3)+d(3)+t(3)
EF(3)=0+15+1.75=15.25 |
4 |
C |
ES(4)=EF(1)=0 |
EF(4)=ES(4)+d(4)+t(4)
EF(4)=0+0+30=30 |
5 |
D |
ES(5)=EF(2)=13 |
EF(5)=ES(5)+d(5)+t(5)
EF(5)=13+0+24=37 |
6 |
E |
ES(6)=EF(3)=15.25 |
EF(6)=ES(6)+d(6)+t(6)
EF(6)=15.25+12+8=35.25 |
7 |
F |
ES(7)=EF(4)=30 |
EF(7)=ES(7)+d(7)+t(7)
EF(7)=30+11+11.33=52.33 |
8 |
G |
ES(8)=EF(4)=30 |
EF(8)=ES(8)+d(8)+t(8)=40
EF(8)=30+10+10=50 |
9 |
H |
ES(9)=Max(EF(5),EF(6))
ES(9)=Max(37,35.25)=37 |
EF(9)=ES(9)+d(9)+t(9)
EF(9)==37+0+6=43 |
... |
... |
|
|
16 |
End |
ES(16)=Max(EF(14),EF(15))
ES(16)=Max(59,55.52)=59 |
EF(16)=ES(16)+d(16)+t(16)
EF(16)=59+0+0=59 |
|
Latest Finish |
| |
The latest finish time
for a node is based on the logical requirement that a node must
end before any of its successors may be begin.
Latest Finish Time = Min(Latest
Start Time for all successors)
The latest start time is the latest finish time,
less the delay time and less the activity time for the node.
We describe these relationships with mathematical
notation below.
The latest finish times and latest start times
are computed in the reverse order of the node indices. First
we set the latest finish time for the End node to the
due time for the project. This must be no less than the earliest
finish time for the project. The latest finish time for a node
must be the minimum of all the latest start times of all successor
nodes. We can compute the latest finish time for a node because
the latest start times for all successor nodes have already
been computed. We illustrate the formulas using columns from
the project worksheet. Recall that although the form does not
show it, the End node has as predecessors all nodes
with no successors. In the example, the predecessors of the
End node are M and N. For the example, the due time
is 59.
Some of the steps of the process are shown in
the table.
Node |
Name |
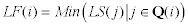 |
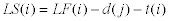 |
16 |
End |
LF(16)=59 |
LS(16)=LF(16)-d(16)-t(16)
LS(16)=59-0-0=59 |
15 |
N |
LF(15)=LS(16)=59 |
LS(15)=LF(15)-d(15)-t(15)
LS(15)=59-0-1.02=57.98 |
14 |
M |
LF(14)=LS(16)=59 |
LS(14)=LF(14)-d(14)-t(14)
LS(14)=59-0-4.5=54.5 |
13 |
L |
LF(13)=Min(LS(14),LS(15))
LF(13)=Min(54.5,57.98)=54.5 |
LS(13)=LF(13)-d(13)-
t(13)
LS(13)=54.5-0-1.5=53 |
12 |
K |
LF(12)=Min(LS(14),LS(15))
LF(12)=Min(54.5,57.98)=54.5 |
LS(12)=LF(12)-d(12)-
t(12)
LS(12)=54.5-1-1.5=52 |
11 |
J |
LF(11)=LS(13)=53 |
LS(11)=LF(11)-d(11)-
t(11)
LS(11)=53-1-9=43 |
... |
... |
|
|
1 |
Start |
LF(1)=Min(LS(2),LS(3),LS(4))
LF(16)=Min(0,1.75,0.67)=0 |
LS(1)=LF(1)-d(1)-
t(1)
LS(1)=0-0-0=0 |
|
Slack Time |
| |
The slack
time is the difference between late and early start times. This
is the same definition as for critical path analysis, but the
calculation of early and late start times now depends on delay.
The figure below shows the results shown previously
and the slack column.
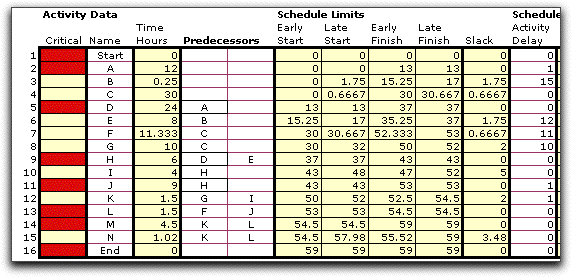
The slack value is the increase the amount of
time an activity can be delayed without delaying the completion
of the project. When the early start time and late start time
are equal, the activity cannot be delayed, so this activity
is said to be critical. Activities with positive slack are not
critical because they can be delayed without affecting the project
duration.
It should be emphasized that the slack of an activity
depends on the delays of other activities in the project. We
can see this by showing the slack and delay columns for several
selections of delays. At the left we see the slacks with all
0 delays, the early start schedule. When we increase the delay
for J, the slacks for all the activities on the critical path
are reduced. Part of the project slack has been used up by the
planned delay. Now, increasing the delay of D to 1 further reduces
the slack along the critical path to 0. In the last figure we
delay I by 4. This activity is not on the critical path, but
the slack for both I and K are reduced since I is a predecessor
of K.
|
Planned Delays |
| |
Planned delays have
importance for scheduling studies because every possible schedule
can be derived by some selection of delay values. We will search
for an optimal schedule by varying the values of the activity
delays.
Delays also have importance in practice. Since scheduling is
done without exact knowledge of how long activities will take,
a schedule with no delays is almost sure to fail. A planned
delay allows time between when the activity may start and when
it is scheduled. Thus if some predecessor activities take longer
than estimated, the delay can simply be reduced and the activity
can start at the scheduled time. Delays serve the purpose of
decoupling the effects of variability in much the same way that
inventory protects a production system from the variability
of demand.
|

|



