An inventory is represented in the simple diagram of Fig. 1. Items flow into the system, remain for a time and then flow out. Inventories occur whenever the time an individual enters is earlier than when it leaves. During the intervening interval the item is part of the inventory.

Figure 1. A system component with inventory

For example, say the box in Fig. 1 represents a manufacturing process that takes a fixed amount of time. A product entering the box at one moment leaves the box one hour later. Products arrive at a rate of 100 per hour. Clearly, if we look in the box, we will find some number of items. That number is the inventory level. The relation between flow, time and inventory level that is basic to all systems is

The flow rate must be expressed in the same time units as the residence time. For the example, we have

Inventory Level = (100 products/hour)(1 hour) = 100 products.

When the factors in this expression are not constant in time, the expression relates time-averaged quantities.

Whenever two of the factors in the above expression are given, the third is easily computed. Consider a queuing system for which customers are observed to arrive at an average rate of 10 per hour. When the customer finds the servers busy, he or she must wait. Customers in the system, either waiting or being served, are the inventory for this system. Using a sampling procedure we determine that the average number of customers in the inventory is 5. We ask, how long, on the average, is each customer in the system? Using the relation between the flow, time and inventory, we determine the answer as 0.5 hours. The relation receives extensive use in queuing analysis where it is called Little's Law.

The relation between time and inventory is important, because very often the reducing the throughput time for a system is just as important as reducing the inventory level. Since they are proportional, changing one factor inevitably changes the other.

The Inventory Level

The inventory level depends on the relative rates of flow in and out of the system. Define y(t) as the rate of input flow at time t and Y(t) the cumulative flow into the system. Define z(t) as the rate of output flow at time t and Z(t) as the cumulative flow out of the system. The inventory level, I(t) is the cumulative input less the cumulative output.

(2)

Fig. 2 represents the inventory for a system when the rates vary with time.

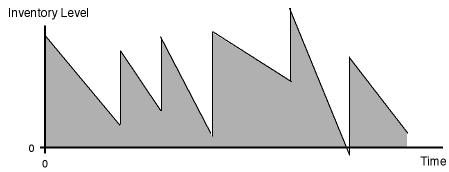
Figure 2. Inventory fluctuations as a function of time.

The figure might represent a raw material inventory. The flow out of inventory is a relatively continuous activity where individual items are placed into the production system for processing. To replenish the inventory, an order is placed to a supplier. After some delay time, called the lead-time, the raw material is delivered in a lot of a specified amount. At the moment of delivery, the rate of input is infinite and at other times it is zero. Whenever the instantaneous rates of input and output to a component are not the same, the inventory level changes. When the input rate is higher, inventory grows; when output rate is higher, inventory declines.

Usually the inventory level remains positive. This corresponds to the presence of on hand inventory. In cases where the cumulative output exceeds the cumulative input, the inventory level is negative. We call this a backorder or shortage condition. A backorder is a stored output requirement that is delivered when the inventory finally becomes positive. Backorders are possible for some systems, while they are not for others. A finished product inventory, for example, may promise later delivery if a customer arrives to find no product available. Alternatively, a customer with alternative suppliers may go elsewhere and the sale is lost. In cases where backorders are impossible, the inventory level is not allowed to become negative. The demands on the inventory that occur while the inventory level is zero are called lost sales.

Variability, Uncertainty and Complexity

There are many reasons for variability and uncertainty in inventory systems. The rates of withdrawal from the system may depend on customer demand that is often variable in time and uncertain in amount. There may be returns from customers. Lots may be delivered with defects causing uncertainty in quantities delivered. The lead-time associated with an order for replenishment depends on the production time of the supplier, which is usually variable and not known with certainty. The response of a customer to a shortage condition may be uncertain.

Inventory systems are often complex with one component of the system feeding another. Fig. 3 shows a simple serial manufacturing system producing a single product.

Figure 3. A manufacturing system with several locations for inventories

We identify planned inventories in Fig. 3 as inverted triangles, particularly the raw material (1) and finished goods inventories (10). Material passing through the production process is often called work in process (WIP). These are materials waiting for processing as in the delays of the figure (2, 4, 6, 8), materials undergoing processing in the operations (3, 7), or materials undergoing inspection in the inspections (5, 9). All the components of inventory contribute to the cost of production in terms of handling and investment costs, and all require management attention.

For our analysis, we often consider one component of the system separate from the remainder, particularly the raw material or finished goods inventories. In reality, rarely can these be managed independently. The material leaving a raw material inventory does not leave the system, rather it flows into the remainder of the production system. Similarly, material entering a finished goods inventory comes from the system. Any analysis that optimizes one inventory independent of the others must provide less than an optimum solution for the system as a whole. We consider inventories that are related by flow in the WIP section of these pages.

Real inventory systems must face the dual curse of variability and uncertainty, and are often embedded in complex systems. In order to develop a theory to help manage inventories it is necessary to construct mathematical models that are abstractions of reality. Every model neglects certain aspects of the problem to obtain results that may be of use. When we describe simplified models on the following pages, we do not actually believe that the models actually are perfectly accurate. On the contrary, if the modeller attemps to create a model to be an accurate reflection of reality it would be too complex to be of value. Simplified models do provide results that can be used for decision-making. Whether a model has sufficient accuracy to make the results valid in a particular context must be judged by those charged with applying the model.