Decision Variables:
Define the variables A, B, and C to
be the pounds of raw materials used, M is the pounds of mix,
and X and Y are the pounds of product.
Constraints:
Conservation of Raw Materials: A +
B+ C = M
Raw Material A restriction: A 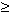 0.45M
0.45M
Raw Material C restriction: C 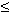 0.3M
0.3M
Product X Definition: X = 0.4M
Product Y Definition: Y = 0.2M
Simple Upper Bounds:
X 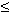 1000, Y
1000, Y 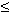 2000, B
2000, B 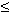 2500, C
2500, C 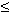 1500
1500
Objective: Maximize Profit
Maximize 12X + 18Y - 1.5M - 6A - 3B
Nonegativity:
A 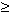 0, B
0, B 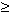 0, C
0, C 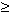 0, X
0, X 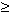 0, Y
0, Y 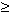 0, M
0, M 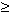 0.
0.
a. The optimum Plan has:
|
A
|
B
|
C
|
X
|
Y
|
M
|
Z
|
|
1125
|
625
|
750
|
1000
|
500
|
2500
|
8625
|
b. Product X is at its upper bound and limiting profit.
The raw material percentage requirements for A and C are also
limiting the profit.
c. From the dual variables, the simple bound with the largest
magnitude is the x limitation with value 8.625 where all others
are zero. From this we see that we would like to increase the
limit on x. We predict the profit will go up by 8.625 for each
unit increase. This return is available as if the allowed amount
of X goes up to 2000.
d. The sensitivity analysis says that the range on this
coefficient is from -6 to 0. Since the coefficients are the
negative of cost, this means that the cost can increase to 6
before changing the solution.
e. From the sensitivity analysis we see that the upper range
on the x limitation is 2000.
f. Raw Material C restriction: 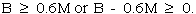
The mix becomes 0. This is the only solution for which the
restrictions are feasible.
Note that it is wrong to say the solution becomes infeasible.
There is no constraint that requires any product to be made
and if no product is made the content restrictions are not effective.
g. The mix is limited by the available amounts of B and
C.
|
A
|
B
|
C
|
X
|
Y
|
M
|
Z
|
|
21000
|
2500
|
1500
|
10000
|
5000
|
25000
|
39000
|
|

