|
|
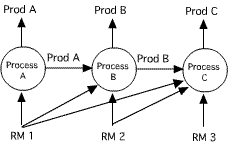
A company makes three products in three processes as shown in
the schematic below. The products are A, B and C. The products
are made with the raw materials 1, 2 and 3. Processes B and C
also require the outputs of the previous processes as input. Each
unit processed in B requires two units of product A, and each
unit of product C requires 1.2 units of product B. Additional
information about the products and raw materials is shown in the
tables. The product revenues are for units sold, not for units
used in other processes.
|
Product
|
A
|
B
|
C
|
Raw Mat.
|
1
|
2
|
3
|
|
Unit Rev.
|
$100
|
$350
|
$500
|
Unit Cost
|
$50
|
$20
|
$40
|
|
Max Sales
|
100
|
150
|
200
|
Available
|
200
|
150
|
200
|
Each unit processed in A requires 1 unit of RM 1.
Each unit processed in B requires 2 units of Product A, 1 additional
unit of RM 1 and 0.6 units of RM 2.
Each unit processed in C requires 1.2 units of Product B, 0.3
additional units of RM 1, 0.2 additional units of RM 2 and 1
unit of RM 3.
Write and solve the linear programming model that finds the
optimum amount of each product to produce and the amounts of
raw materials used. The goal is to maximize profit.
|

