Three products can be produced at two machining centers. The products
may be produced in fractional amounts. The linear relationships
describing this situation are listed below. The variables are:
A, B and C are the amounts of the three products in units.
R1 and R2 are the amounts of raw materials
used in kilograms.
T1 and T2 are the times used in the
two machining centers.
|
Profit:
|
P = 20A + 30B + 25C - 6R1 - 8R2
|
|
Time required on machine 1:
|
T1 = 5A + 8B + 10C (hours)
|
|
Time required on machine 2:
|
T2 = 8A + 6B + 2C (hours)
|
|
Raw material 1 used:
|
R1 = 1A + 2B + 0.75C
|
|
Raw material 2 used:
|
R2 = 0.5A + 1B + 0.5C
|
|
Market Limits:
|
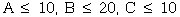
|
We have three goals listed in order of priority below. These
are not strict limits, but only goals.
Goal 1: The minimum production of the three products is to
be equal to at least 5 units.
Goal 2: The profit should be at least 150.
Goal 3: The total time used on the two machines should be
no more than 150 hours.
Write the complete linear programming model that will solve
this goal programming problem. Include the strict constraints
that each machine can operate no more than 100 hours individually.
Solve the problem to find the optimum production quantities.
|

