a. For convenience express the objective as
a minimization and add the cost of additional plant use.
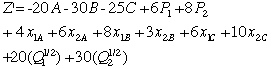
To determine the effect of the addition we note that the nonlinear
terms are separable and all of the same form. To determine the
convexity we compute the second derivative.
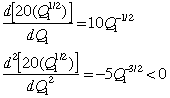
Since this is negative, the minimization objective is not convex
and the algorithm does not yield a global minimum.
The constraints of the problem must also be modified to account
for the increased production.
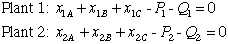
b. We restate the constraint as a greater than or equal to
constraint, and we compute the Hessian matrix for the quadratic.
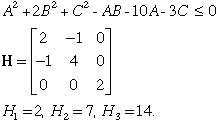
The matrix is positive definite, and the constraint is convex.
The solution will be a global minimum.
c. This is a nonlinear equality constraint. The fact that it
is an equality constraint makes the feasible region nonconvex.
The solution therefore may be a local minimum.
|



