| |
-
|
When this
add-in is installed, a new item appears on the OR_MM menu, LP/IP
Solver. This item does not solve models. Rather, models are
solved when the user clicks on the Solve button on
the linear, integer, or mixed integer model sheets. The LP/IP
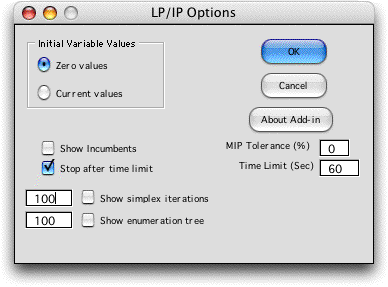
Solver menu item presents a dialog that sets several parameters
related to the solution process and displays. The dialog will
appear only when a mathematical programming model constructed
with the Math Programming add-in is present on the active worksheet.
Otherwise the message below indicates that it is not available.
"This is not a valid worksheet for the
LP/IP Solver"
When a valid worksheet is active, choosing the LP/IP Solver menu
item presents the dialog below. These options only affect the
Jensen LP/IP Solver, and do not affect the Excel Solver.
|
| |
Solution Display Options |
| |
These
options create a separate worksheet for algorithm details that
shows iteration information from the solution algorithms. The
reports are useful for the student who is learning about the
solution methods used. They may also be useful for practitioners
trying to discover why certain IP models are so hard to solve. |
| |
Simplex
Iterations
This option creates a new worksheet with the suffix Details.
Information about the iterations of the primal simplex is
printed on this worksheet. The number field to the left on
the dialog holds the number of iterations to be displayed.
Since some problems may require thousands of iterations, this
number should be set to a reasonable value or the memory requirement
for Excel will be excessive.
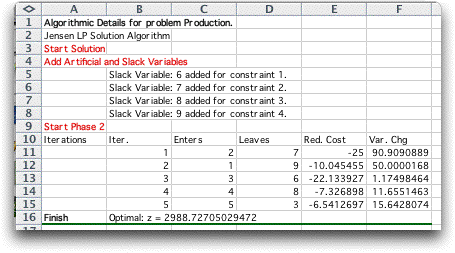
The figure below shows the detail worksheet for the Production problem
described earlier. The display shows the slack variables added
for the four constraints. No artificial variables are required.
Five simplex iterations are necessary to find the optimum solution.
The display shows details about the iterations.
|
| |
Enumeration
Tree
When the production variables are required to be integer,
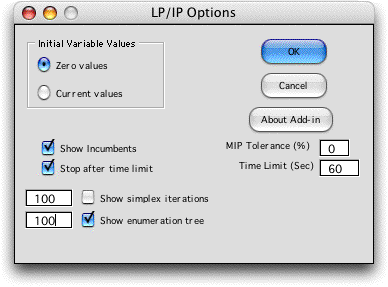
the LP/IP add-in can be used to show the details of the enumeration
process. Using the LP/IP Solver dialog we click the Show
Enumeration Tree checkbox. The number field to the left
on the dialog is the number of enumeration tree vertices to
be displayed. We have also checked the Show Incumbents checkbox.
While the problem is solved a record is kept of the enumeration
process and displayed on the Details worksheet. The
production problem with integer variables requires an enumeration
tree with 42 nodes.
Clicking both display checkboxes will show both
the enumeration tree and the corresponding steps of the simplex
method used by the bounding procedure.
|
| |
The
solution of the problem is below. Cell F4 shows the profit
associated with the best solution found (the final Incumbent).
Cell F5 shows the upper bound on the profit. In this case,
the solution is optimum and the upper bound has the same value
as the incumbent.
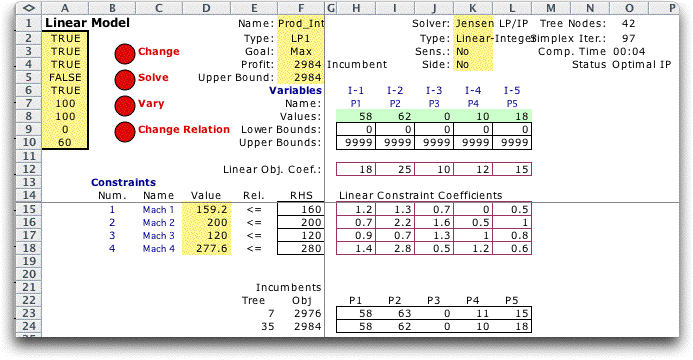
Below the model we show the incumbents discovered during the
procedure. The first feasible solution was found at node 7
of the enumeration tree. The second, and final, feasible solution
was found at node 35. It is often useful to view the incumbents
in this manner. Integer and mixed-integer problems sometimes
have many similar solutions and viewing the incumbents may
show this. |
| |
Algorithm Control Options |
| |
Initial
Variable Values
Two different starting strategies are available. The first
option starts with all variable values equal to 0. The second
strategy gathers the initial variable values from the values
shown on the worksheet. The algorithm starts with these values.
This advanced start option reduces the number of iterations
required when only slight modifications are made to the model.
When the model is an IP or MIP and the initial solution is
feasible, the solution add-in uses this solution as the initial
incumbent. A good initial solution often reduces the size of
the enumeration tree and the time required to solve the problem.
When the example uses the optimal solution for the initial
solution, the enumeration tree has only 16 nodes. The tree
is shown below. |
| |
|
| |
MIP
Tolerance
When solving integer or mixed integer programming problems,
vertices of the enumeration tree are fathomed when the relaxed
solution objective is less than (for a maximization problem)
than the incumbent solution. A nonzero tolerance makes the
fathoming test a little easier by fathoming the vertex if its
relaxed objective is within x% of the incumbent solution, where
x is the number entered in this field. The solution may be
found with fewer iterations and less time when this value is
greater than 0. When the tolerance is other than 0, however,
there is no guarantee that the optimum solution is obtained.
It is guaranteed that the solution is with x% of the optimum.
The Excel Solver has a similar tolerance specified in the Options
dialog of the Solver.
In the dialog below we specify a 1% tolerance level.
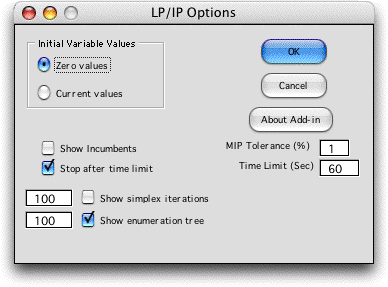
|
| |
Clicking
the Solve button provides the following solution. The
solution returned is not optimum. Rather the solution has the
profit of 2976. The optimum has the profit of 2984. The upper
bound returned in cell F5 is 2988. One of the primary features
of the solution procedure is that it returns both lower and upper
bounds on the solution value. Although the selection of 1% in
for the example does not result in a guaranteed optimum, we are
guaranteed that the solution is 1% of the optimum. The objective
for the incumbent and the Upper Bound value provides
a range in which the optimum value must reside. |
| |
|
| |
The
advantage of choosing a nonzero tolerance is that the size of
the tree is significantly reduced. For the example the tree is
reduced from 42 to 14 nodes. For larger problems, the reduction
will often be a much greater proportion. |
| |
|
| |
Time
Limit
When solving all integer or mixed integer programming problems,
the process may take a long time. The program will stop when
this time limit is reached. The user may give up at this point
or continue the optimization. The Excel Solver has a similar
time limit specified in the Options dialog of the Solver. |
| |
Show
Incumbents
When solving all integer or mixed integer programming problems,
the algorithm may find feasible solutions during the enumeration
process. During the process, the feasible solution with the
best value is called the incumbent solution. When
the process is complete, the final incumbent is placed on the
worksheet as the solution. When this checkbox is selected,
all incumbents discovered are shown below the model. This is
illustrated in a figure above. |
| |
|



