 |
We illustrate
the model for the CTMC version of the queuing process.
The data form has a single red button. The Build
Model button
calls the DP
Models add-in to insert the model worksheet and
construct a general model. The DP Data add-in then
fills the form to describe
the queue model. If you are not interested in the modeling
process you may proceed by clicking the Transfer to Markov
Analysis button.
This button calls the Markov Analysis add-in for further
analysis. The Transfer to
DP Solver button calls the DP Solver add-in.
The Markov
Analysis add-in has more analysis options that the DP
Solver add-in, but the DP Solver add-in can deal
with larger problems. Although at first the model form appears
to be complex, the user really not be concerned about the form.
It is automatically constructed and filed with the necessary
formulas by the add-ins.
The model part of the worksheet is shown below. Generally
yellow cells hold formulas that should not be changed and white
cells hold parameters that define or limit the model. Cells
with a red outline are changed by the DP Data add-in to replace
default vales. |
|
States and Events |
| |
The figure shows the
states and events at the top of the model. There is a single
state variable measuring the number in the system.
The single event has three values: -1 for service completion,
0 for no event (Null), and +1 for arrival. The figure shows the
state is 0 and the event is 1, indicating an arrival. The information
for the event rate and cost comes from a table constructed to
the right of the model and shown below.
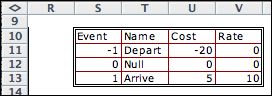
The entries in the rate portion of the table
are governed by formulas that depend on the state. When the
state is 0, the departure event is impossible, so the rate
shown in V11 is 0. Similarly the rate depends on whether the
number in the system is less than or equal to the number of
servers. The expression in V11 is the formula shown below.
It is complicated, but it serves to compute the rate of departure
as a function of the state of the system.
=IF(FQ_1_DPM_State < FQ_1_DPM_Num_Servers,
FQ_1_DPD_Mu*FQ_1_DPM_State,
FQ_1_DPD_Mu*FQ_1_DPM_Num_Servers)
|
Transitions |
| |
There are two transition blocks. The
first computes the transition caused by a balk. It is only effective
when the state is at its maximum value and the event is an arrival.
The second block takes cares care of all other cases. |
Enumeration |
| |
When the model is transferred
to the Markov Analysis add-in, the program enumerates
all states and events to find the set of all states with their
cost rates and all events. |
|
| |
The combination of
states and events determines the transition list. For the CTMC
only transitions with nonzero rates are listed. |
| |
|
| |
The
state, event and transition lists are the outputs of the
DP Models add-in.
This data is sufficient to define the Markov chain. The data
for the model is entirely linked to the data in the queuing data
table constructed by the DP Data add-in. The casual
user of the model described on this page need not
interact with the model form. Every necessary function is performed
by one of the add-ins. Changing the data on the table immediately
changes the affected cells on the model form. When the model
form is changed, it is necessary to rebuild the markov chain
model. |
Build Matrix Model |
| |
A CTMC model is created
by clicking
on the Transfer to Markov Analysis button.
Then the Markov
Analysis add-in constructs the appropriate Excel worksheets
and the DP Models add-in inserts the data defined
by the model. The rate matrix model for the
example is shown below. |
|
| |
The economic transition
matrix is also constructed. The state cost rates are in column
E and the transition costs for arrivals and departures are in
the matrix starting at column H. The balking cost is at the lower
right cell of the matrix. |
|
| |
The Markov Analysis
add-in allows several different analysis as indicated
by the buttons on the Matrix page. The steady-state
results are shown below. |
|
Summary |
| |
This page demonstrates
the CTMC model for the finite queue. The DP
Data add-in constructs a table holding data for the model.
By clicking the Build Model button on the data
page, the DP Models add-in constructs the model
worksheet and it is filled with the constants and formulas that
implement the model. By clicking the Build Matrix Model button,
the Markov Analysis add-in builds the rate and
economic transition matrices and inserts the values describing
the system. All three add-ins must be
installed for all the steps to work.
The DTMC model is similar to this one, but the model generates
transition probabilities rather than rates. The MDP version
of this problem adds a decision that increases or decreases
the number of service channel based on the current state of
the system. The MDP model includes optimization as part of
the stochastic model. |
| |
|



