 |
The problem addressed in this
section is the allocation of scarce resources to alternative
activities. The problem is often used as an introduction to
dynamic programming.
The resources problem, as this is page is written, is only
available for the deterministic dynamic programming, DDP. As
often is true for DDP models, there is a math programming model
that more effectively solves the linear version of this problem.
We describe the math programming model below. The amounts
of left over resources are modeled explicitly so that resources
not used in the allocation can be given a nonzero value.

Written as a mathematical program, the resource
problem is:
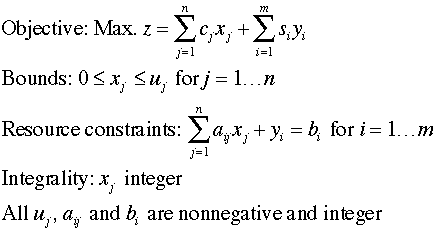
This is the linear version of the problem that
for most instances is easily solved by math programming solution
techniques. The add-in creates a DP version of the problem.
It can handle separable nonlinear as well as linear models |
Data for the Resource Model |
| |
|
We create the model by choosing Data from
the DP Data menu. The model selection dialog is
presented. Here we consider the Resource problem
with a deterministic DP model. When this page is written,
only the DDP model is available. |
|
| |
|
Fill the name field with a
short name with no spaces or punctuation. The name, number
of items, and number of resources
are fixed once the worksheet is created. The maximum
of each item can be changed on the data worksheet.
By checking the Make Random Problem box,
the model parameters are assigned randomly. The Maximize
Objective button determines the direction of optimization. |
|
| |
The data form is below. The yellow
cells should not be changed. The white cells can be changed to
reflect the current problem. The data shown was randomly generated
using a fixed seed. This example has only one resource and four
items. |
| |
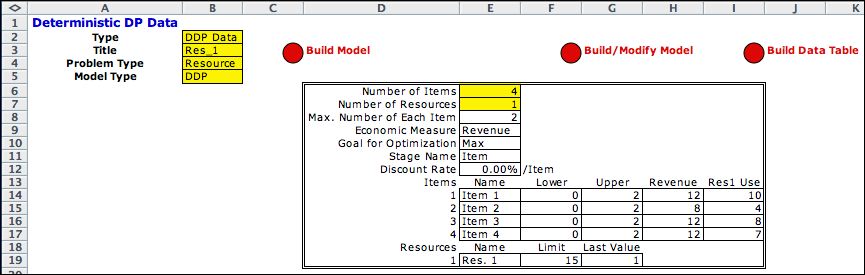
|
| |
Clicking the Build Model button
on the top of the data worksheet, calls the DP Models add-in
to construct the model worksheet. The Build/Modify Model button
also constructs the model worksheet, but first presents the Model dialog.
This allows the model parameters to be modified by the user.
Clicking the Build Data Table button constructs tables
for the revenue and resource use data. This allows the representation
of nonlinear forms. |
The Math Programming Model |
|
|
The math programming model is shown below as constructed
by the Math Programming add-in. Although the problem has only
one constraint, the default minimum for the add-in is two
constraints. The second dummy constraint is not restricting. The
model has four integer variables representing allocation amounts.
The fifth variable is the unused resource. |
| |
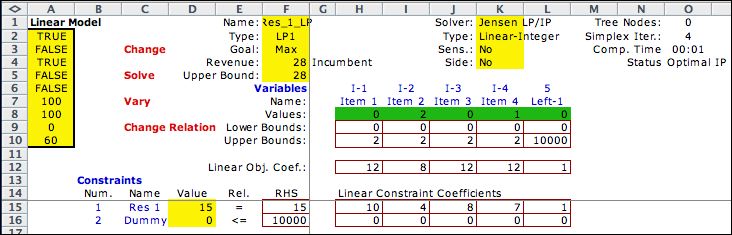
|
| |
The optimum solution two units of
item 2 and one unit of item 4. The objective is 28 and all the
resource is used. |
The Table Option |
| |
A two constraint data
table is below with data provided by random integer values. |
 |
| |
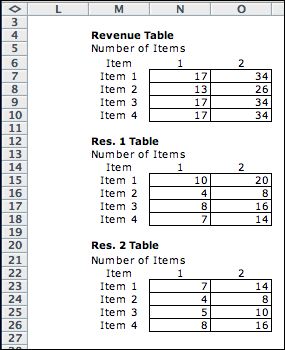 |
Clicking the Build Data Table button
calls the add-in to make tables for benefits and resource
use as a function of the number of items selected. The
tables take data from the linear data table for the first
item.
The second item terms of the table are 2 times the first
item value. Thus, the original table values represent the
linear problem. The values in the table can be changed however,
to show any separable nonlinear function of the number of
items. Since
the DP algorithms enumerate all possible solutions, the linearity
of the revenue or resource usage terms has no affect on the
model. |
|
|
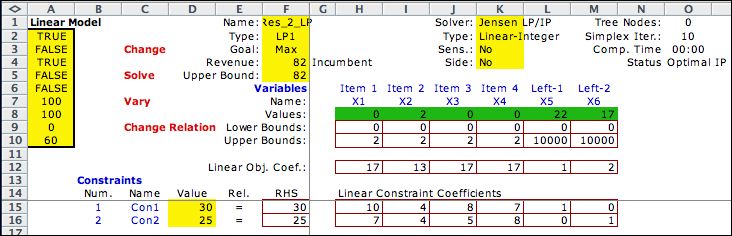
The math programming
model for the two constraint linear problem is shown below. The
solution uses two of item 2. The remainder of the resources
(22 and 17) is left over. Apparently, the values of assigning
the resources to one of the remaining alternatives is not justified. |
| |
|
| |
The DP model and
solution are described on the next page. |
| |
|



