|
|
 |
Random
Variables |
 |
-
User Defined Functions |
 |
With
the Random Variables add-in, several functions are provided for
dealing with probability distributions. They are found in the
User Defined list of the Excel function list. Each function has
the prefix RV. We present the general definitions below, with
examples taken from the dice random variable. The example is shown
in both the numerical format and the formula format, so you can
see how to enter the functions. |
| |
|
| |
User Defined Functions
| Function |
Purpose |
RV_prob(RV,Lower,Upper)
RV_prob(Dice,B8,B9) |
Computes the probability that the random variable RV
falls between Lower and Upper, inclusive.
For the example, the statement points to cells B8 and
B9 where the numbers 8 and 10 are stored. The function
returns the numerical value of 0.333, the probability
that a throw of the dice will yield between 8 and 10,
inclusive.
Rather than name the random variable as in the example,
the user can select a range that includes the type of random
variable and its parameters. The Lower and upper parameters
may be left out. For instance
RV_prob(RV,,Upper)
will return the probability that the random variable is
less than Upper. |
RV_inverse(RV,Prob)
RV_inverse(Dice,B11) |
Computes the value of the random variable, such that
the probability that RV is less than that value is equal
to Prob.
The example points to B11 where the number 0.8 is entered.
The value of the cumulative distribution at 9 is 0.8333.
The function returns 9 because it is the smallest value
whose cumulative distribution exceeds 0.8. |
RV_mean(RV)
RV_mean(Dice) |
Computes the mean of RV. |
RV_var(RV)
RV_var(Dice) |
Computes the variance of RV. |
RV_skew(RV) |
Computes the skewness of RV. This is computed as the third
moment about the mean squared, divided by the variance cubed.
This method corresponds to the formulas used by Excel to
compute the skewness of statistical data. |
RV_kurt(RV) |
Computes the kurtosis of RV. This is computed as the fourth
moment about the mean divided by the variance squared. This
method corresponds to the formulas used by Excel to compute
the kurtosis of statistical data. |
RV_simV(RV)
RV_simV(Dice) |
Simulates RV. The function name ending in V indicates
that this function is volatile. Each recompute of the worksheet
simulates a new value. This is useful in Monte-Carlo simulation
studies. |
RV_sim(RV,
Seed) |
Simulates RV with a seed. This option allows a repeatable
sequence of random observations. A negative seed determines
the first value. A positive seed gives the next simulated
value in a sequence. |
|
| |
Each function
has an argument which specifies a range showing the type and
parameters of the random variable, shown below as RV. This
may be the name of a previously defined random variable. In
this case, RV is typed as a word, such as "Dice" (without
the quotes). |
Examples of User Defined Functions |
 |
| RV_prob(RV,Lower,Upper) |
This function computes
the probability that the random variable specified by the
first argument falls within the limits specified by the
last two arguments. Lower is a number or reference to a
number that specifies the lower bound of the range. If no
value is specified, Lower is taken as the smallest number
the random variable can assume or negative infinity if the
random variable is unbounded from below. Upper is a number
or reference to a number that specifies the upper bound
of the range. If no value is specified, the value is taken
as the largest value in the range of the random variable
or positive infinity if the random variable is unbounded
from above. Several examples are shown below for the Craps
game. The first column is the event, the second is the expression
entered into the cells, and the third is the value. |

|
 |
|
Distribution
information may be entered by reference rather than name
in the Probability function and the other functions of
this section. Say the array of numbers shown below is
placed on worksheet in column A.
Entering " = RV_prob(A1:A4,2,3)
" into a cell computes the probability that the random
variable with a discrete triangular distribution will
fall between 2 and 3, inclusive. The names for the distributions
are the same as those appearing on the Distribution Dialog
sheet shown above. Identifying a distribution by reference
is useful when the distribution data is entered in a row
or column of a spreadsheet. |
| RV_inverse(RV,Prob)
|
This function computes
the inverse probabilities of defined random variables. The
random variable name is specified in the RV argument. The
probability is specified in the Prob argument. The function
returns the smallest value of x such that P(RV <= x)
<= Prob. As an illustration of inverse probabilities
assume that the time required for a given activity has a
Normal distribution mean of 2.5 hours and a standard deviation
of 1 hour. Several examples of inverse probabilities are
given below. We ask, how much time must we allow to assure
with 90% probability that the activity is complete? From
the first of the three examples we conclude that 3.78 hours
must be allowed. |

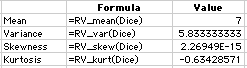
| RV_mean(RV)
RV_var(RV)
RV_skew(RV)
RV_kurt(RV) |
These functions compute
four moments of the distribution, the mean, variance,
skewness and kurtosis. Moments for the Dice random variable
are shown below. |
The example below shows
the moments computed for a binomial random variable. The negative
sign on the skewness indicates that the distribution is skewed
to the left. A positive sign indicates a distribution skewed
to the right.

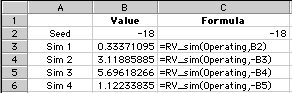
| RV_sim(RV,
Seed) |
This function simulates
values of the random variable. RV is the name of the random
variable, and Seed is a number or reference to a number
which is a seed for the internal random number generator
of Excel. The table below shows the set of commands that
generates a series of four simulated values of the Operating
random variable defined above. By providing a negative
number as the seed, a repeatable series of simulated values
is obtained. This is useful in a many contexts. |
| RV_simV(RV)
|
This function simulates
values of the random variable. This is a volatile function,
in that every time the cell is recalculated, a new simulated
value of the random variable RV is presented. No seed
is necessary. The example shows the simulation of 5 throws
of a pair of dice. |

|
| |
|
|



