|
|
The examples for this section are in the demo workbook
(teachip_benders.xls). To solve or change the model
or construct a new model, you must have the Teach
IP add-in loaded. The Jensen LP/IP Solver add-in must
also be loaded. Use the Relink buttons command to
establish links to the worksheet buttons.
We do not provide a complete description of the algorithm
here. Download the PDF Bender's
Algorithm document for details.
It is easy to run the algorithm. Create a Benders'
model from the Teach IP menu. Click the Setup button
on the worksheet. Click the button to Do Benders'
Algorithm. Then click the Solve Dual button. Then
sequentially click the Solve Master Button and Solve
Dual buttons until the bounds become equal.
|
Problem Definition
Begin a Benders' problem by clicking on the
Benders item on the Teach IP
menu. The program presents the problem definition dialog to
accept model data.
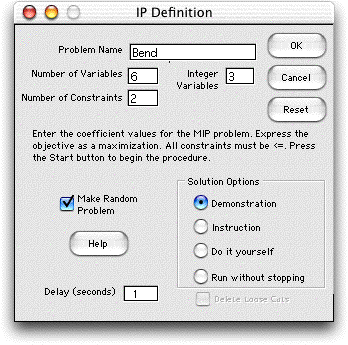
The program presents a possible name in the
Name field such as TeachIP1. There can be multiple
IP models in a workbook, and the integer number at the end
of the name will advance as IP models are added. The name
is used as prefix for a number of named ranges on the worksheet,
so once the name is specified it should not be changed. Names
must obey the Excel rules for naming ranges. The name should
begin with a letter, and include no spaces or punctuation
marks (a period is OK). The underline symbol may be used and
is often handy for two-part names such as P_1. A name like
P1 can't be used because it can be confused with a cell reference.
Fields are available for number of variables,
number of constraints and number of integer variables.
If the latter is fewer than the number of variables, the variables
with the smaller indices are assumed integer. For a reasonable
demonstration, keep the numbers of variables and constraints
small. The model must be expressed as a maximization. For
Benders' algorithm some variables must be real and some must
be integer. If the Make Random Problem box is checked,
the program will provide random coefficients for the objective
function and constraints. Bender's problems must have only
less than or equal to constraints. All coefficients are integer
and positive. A random problem will always have a feasible
solution. When the model is displayed the student can change
any of the data.
One of four modes of operation is chosen with
a button in the Solution Options frame.
- Demonstration Option: In this mode, the program
takes the student through the steps of the procedure. Message
boxes describe the steps as they occur. The student presses
OK buttons to progress.
- Instruction Option: This is almost the same as
the the next option, but the program places the active line
at each the Dual or Primal problem as appropriate.
- Do it Yourself Option: The student must make all
the decisions directing the algorithm.
- Run without Stopping Option: The program runs the
procedure with no student interaction.



