The Artificial Start
The primal simplex method requires an initial solution that
is basic and feasible. A basic solution for the minimum cost
flow network problem is identified by a graphical structure
called a tree. A tree is a set of arcs that has no cycles.
The initial tree consisting of artificial arcs is shown in
the figure below.
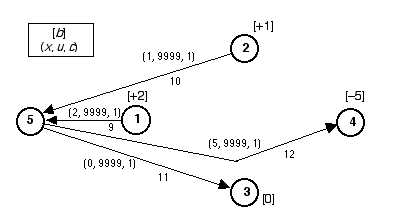
Arc
Display with Artificial Arcs
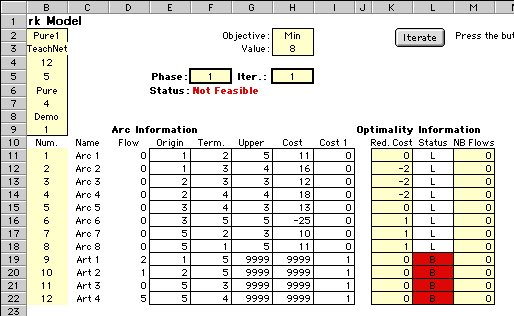
After pressing the Iteration button on the worksheet,
the initial flows are assigned to the artificial arcs as shown
in the arc display. Remember that in the first
arc display all the artificial arcs were directed out
of node 5. In this display arcs 9 and 10 have been reversed
in direction to enter node 5. Here we see the purpose of the
artificial arcs. They carry the fixed external flows at the
nodes in the first iteration. We also see that arcs which
formerly touched only one node in the network, arcs 6, 7 and
8, now either originate or terminate at the slack node. The
slack node has the ability to supply or absorb any amount
of flow. For this pure problem (all gains 1), the slack node
must supply +2 units of flow.
In the figure above, the costs for the artificial
arcs are 1. When the simplex is applied with artificial arcs,
the algorithm is applied in two phases. In phase 1, the artificial
arcs have costs of 1 and all the original arcs have costs
of 0. On the worksheet, these are in the column labeled Cost
1. As the algorithm progresses, if a feasible solution exists
for the original problem, the minimum cost solution will have
zero flow on the artificial arcs and all nonzero flows on
the original arcs. This is the purpose of phase 1, that is
to find some solution that is feasible to the original problem.
The solution shown on the arc display is feasible when the
artificial arcs are included, but not feasible otherwise.
The total cost of this solution is 8.
If phase 1 ends with nonzero flows remaining
on artificial arcs, there must be no feasible solution for
the original problem. In this case the algorithm ends with
a message that no feasible solution exists.
Node
Display with Artificial Arcs
We use this display to explain the information
shown on the worksheet. Note that most of the columns of the
display are colored yellow. These columns contain formulas
or are filled by the program. They are not to be changed by
the user.
- Fixed: This range holds the fixed external flows
of the original network. The fixed flow of the slack node
has been assigned the value of 2 to balance the external
flows of the other nodes.
- Balance: This range holds a formula that computes
the net flow at each node. For a solution that obeys the
conservation of flow requirement, the range should have
all zeros.
- Adj. Ext.: The abbreviation stands for Adjusted
External Flows. When some of the nonbasic arcs have flows
equal to the upper bounds, the fixed external flows must
be adjusted at the nodes to reflect these nonbasic flows.
This range holds the adjusted flows.
- Basis: This range holds the indices of the basic
arcs. In the first iteration the indices are the artificial
arcs. Note that some of the indices are negative. We always
arrange the basic arcs so that the arcs form a directed
tree rooted at the slack node. To do this, some arcs must
be used in the reverse direction, as arcs 9 and 10 for the
example. These are called mirror arcs. Arcs that are not
reversed, such as 11 and 12, are forward arcs.
- Origin: This range holds the origin nodes of the
basic arcs.
- Term.: The abbreviation means Terminal. The range
holds the terminal nodes of the basic arcs.
- Lower: These are the lower bounds for flow on the
basic arcs. The number is 0 for forward arcs. For a mirror
arc the lower bound is the negative of the upper bound for
the corresponding original arc.
- Upper: These are the upper bounds for flow on the
basic arcs. The number is given in the upper bound data
on the arc display for forward arcs and 0 for mirror arcs.
- Cost: This range holds the unit costs for the basic
arcs. In phase 1, the artificial arcs all have costs of
1 and the original arcs have costs of 0. The cost on a mirror
arc is the negative of the corresponding cost on the forward
arc.
- Dual: This range holds the dual values for the
nodes. The dual value of the slack node is zero, and the
dual values for all the other nodes are determined by the
complementary slackness equation.
- Flow: This range holds the flow values for the
basic variables. These are the flows required for conservation
of flow at the nodes. Note that the flow in the mirror arcs
is the negative of the flow in the corresponding original
arc.
- Delta and Ratio: These columns are used
to determine the arc that is to leave the basis in the simplex
procedure. We discuss them on the next page where we consider
the basis change activity.



