Models - Operations Research Models and Methods

Models

Dynamic Programming

Investment Problem

Problem Statement

DP Approach

DP Finish

	Investment Problem
	Problem Statement

A portfolio manager with a fixed budget of $100 million is considering the eight investment opportunities shown in Table 1. The manager must choose an investment level for each alternative ranging from $0 to $40 million. Although an acceptable investment may assume any value within the range, we discretize the permissible allocations to intervals of $10 million to facilitate the modeling. This restriction is important to what follows. For convenience we define a unit of investment to be $10 million. In these terms, the budget is 10 and the amounts to invest are the integers in the range from 0 to 4.

Table 1. Returns from Investment Opportunities
Amount	Opportunity
Invested ($10 million)	1	2	3	4	5	6	7	8
0	0	0	0	0	0	0	0	0
1	4.1	1.8	1.5	2.2	1.3	4.2	2.2	1.0
2	5.8	3.0	2.5	3.8	2.4	5.9	3.5	1.7
3	6.5	3.9	3.3	4.8	3.2	6.6	4.2	2.3
4	6.8	4.5	3.8	5.5	3.9	6.8	4.6	2.8

Table 1 provides the net annual returns from the investment opportunities expressed in millions of dollars. A ninth opportunity, not shown in the table, is available for funds left over from the first eight investments. The return is 5% per year for the amount invested, or equivalently, $0.5 million for each $10 million invested. The manager's goal is to maximize the total annual return without exceeding the budget.

The investment problem has a general mathematical programming formulation.

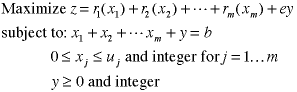
The notation is the general model is defined below.

The problem as stated is similar in structure to the knapsack problem but the objective function is nonlinear. To formulate it as a mixed-integer linear program it would be necessary to introduce 32 binary variables, one for each nonzero level of investment. Since the budget and investment amounts are integer the slack variable, y, can be treated as integer. Rather than pursuing the MILP formulation we will use the problem as an introduction to dynamic programming.