To illustrate the data feature of the add-in, we obtained the monthly unit values for the asset funds of the CREF annuity investment account. This account is administered by TIAA-CREF. The data for one year is shown below.

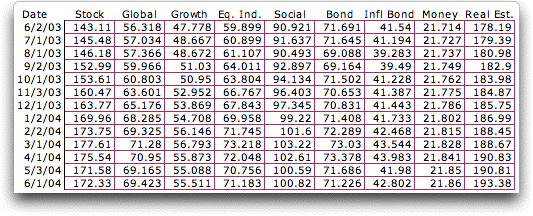
We compute the monthly return for each fund with the formula:

100*(BV - EV)/BV

BV is the unit value at the beginning of the month, EV is the value at the end of the month. We multiply by 100 to express the returns as percentages. The resultant table of returns is below. The table is in the format of the Equity add-in. The number of periods (months) per year is 12.

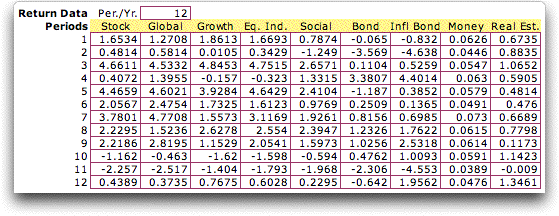
Statistical analysis, using Excel statistical functions, computes the fund average returns and standard deviations. The formulas for the Stock fund are below. Returns and standard deviations are annualized using the Cref_Per_Yr variable (12 in this case). For example, the Stock fund provided almost an 19% return for the year. The annual equivalent of the standard deviation of the Stock data is 7.3745.

=CREF_Per_Yr*AVERAGE(CREF_Return1)
=SQRT(CREF_Per_Yr)*STDEV(CREF_Return1)

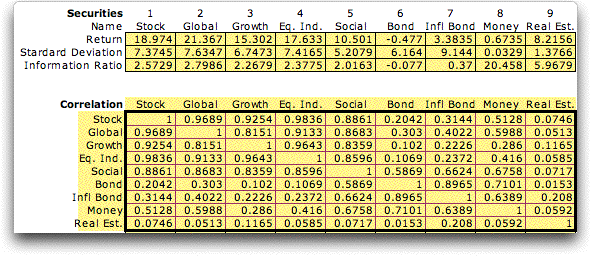
The correlation matrix is computed from pairs of data columns using the Excel CORREL function. Note that all the correlations are positive in this case.

Solutions on the efficient frontier with ten intervals are found using the add-in.

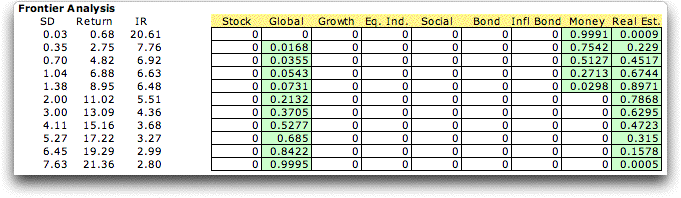
The return and standard deviations for eleven solutions determine the efficient frontier graph.

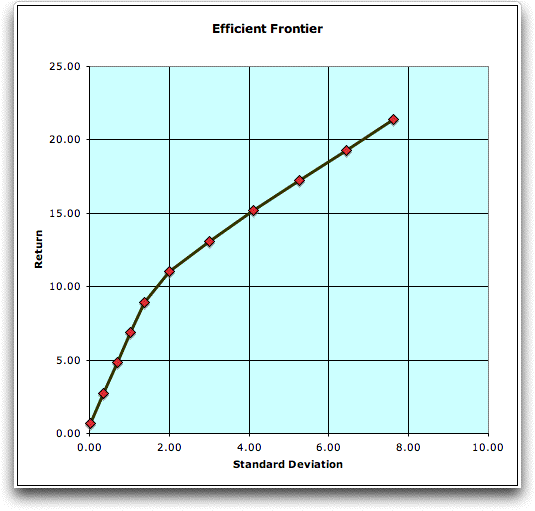
The minimum variance portfolio uses only the Money Market investment (the first solution shown is not quite the minimum variance solution). The maximum return solution (with maximum variance) invests in only Global Equities. Intermediate solutions use a combination of Money Market, Real Estate and Global Equities. The best portfolio for a specific investor depends on his or her risk preference. Our example uses only one year of data. The results would probably change if a longer history were used.

ETF Example

This example constructs a portfolio out of 14 Exchange-Traded Funds (ETFs). The funds are designed to track market indices from several market segments as in the list below. The funds are traded under the Ticket symbols listed.

Five years of monthly data from 1999 to 2004 were used to compute the annualized mean return and standard deviation for each fund as shown in the figure. The correlation matrix is also computed from that data. The statistical results appeared in the paper: "Jackknife Estimators for Reducing Bias in Asset Allocation" by Amit Partani, David Morton and Ivilina Popova, in Proceedings of the 2006 Winter Simulation Conference. In this case the returns, standard deviations and correlations were computed externally to the add-in. Only the bottom half of the correlation matrix must be entered. The top half is computed through equations that point to the appropriate entry in the bottom half.

Clicking the Frontier button, presents the sequence of eleven solutions on the efficient frontier, ranging from the solution with the lease variability to the one with the greatest return.

The graph of the standard deviation and return for these solutions describes the efficient frontier.