| The Problem |
| |
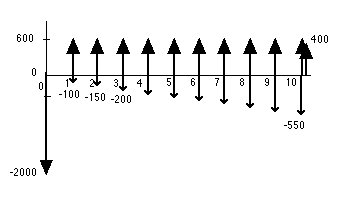
A businessman is considering
the purchase of an asset that has an initial cost of $2000.
The asset promises an annual return of $600. It's operating
cost is $100 the first year, $150 the second, and increases
by $50 in each subsequent year. The salvage value for the asset
in 10 years is $400, or 20% if its initial cost. The cash flow
for this situation showing the individual components explicitly
is shown in the figure below. If the businessman's minimal acceptable
rate of return is 10%, should he invest in this project?
|
The Project |
 |
|
Install
the Economics
add-in. Choose Add Project from the menu.
Fill in the dialog with the number of
cash flows (3, one for the revenue, one for the uniform part
of the operating cost, and one for the gradient part of the
operating cost). Fill in the number of investments (1 for the
2000 investment at time 0). Fill in the Minimum Acceptable Rate
of Return (MARR = 10%) and Life (10 years). These can be changed
later. The bottom half of the dialog is used when taxes and/or
inflation is to be modeled. |
| |
|
| |
The add-in creates
a form with some items filled in. Specify the investment in
row 8 as a negative number. The Salvage is the percentage
of the investment that is returned at the end of the life of
the asset (20% = 400/2000). The Start value indicates
when the asset is put into service and the End value
indicates the end of its life.
The return is entered in row 11 as a uniform series with value
600. The first payment time (at the end of year 1) is entered
in the Start cell and the last payment time (at the
end of year 10) is entered in the End cell. The uniform
part of the operating cost is entered in row 12 as a negative
number (-100). The operating cost is increasing by an amount
$50 per year. This is entered as a negative gradient (-50)
in row 13. The Start cell indicates when the first
non-zero payment occurs (2) and the End cell indicates
when the last payment occurs. The Parameter for the
gradient is the periodicity of the payments (1 means that it
occurs annually). All the words and numbers in the white cells
can be changed. |
| |
|
The Results |
| |
The yellow cells in
column Q are computed by formulas inserted by the add-in. These
are the results of the analysis. Cell Q8 is the present worth
of the investment considering both the amount of the investment
and the salvage. Cells Q11 through Q13 hold the present worths
of the annual cash flow components.
Cell Q2 holds the sum of the investment and cash flow present
worths. The is the net present worth of the project over its
life. Since the value (81.93) is positive, the investment returns
more than 10%, the MARR. This implies that the investment should
be acceptable to the decision maker. A negative value implies
that the project does not return the MARR. Cell Q3 holds the
equivalent net annual worth of the project. It is also positive
because it is proportional to the net present worth. Cell Q4
holds the present worth over the study period. Since the study
period (10) is the same as the life, this is the same as the
present value over the life. |
The Internal Rate of Return (IRR) |
| |
|
The internal rate of return is
the interest rate that makes the net present worth of the project
equal to zero. It is a measure of the profitability of the
project. It is discovered by a binary search procedure. Selecting Compute
Rates presents the dialog below. The project E6_2 is selected
from the Name field.
For some projects there may be more than one solution that
yields a zero net present worth. Different solutions may be
found by specifying the initial guess and range of the search
process. The example is called a simple investment since a
single investment is followed by net revenues in the following
years. This kind of investment has only one solution for the
IRR. |
| |
|
| |
The add-in successively
changes the MARR in cell O1 until the IRR is determined. The
rate is placed in cell Q5 on the project definition. It is
colored green to indicate that the number is computed by an
algorithm. If some of the parameters of the project are changed,
the yellow cells will automatically compute new values. The
IRR cell will not change, however, unless the algorithm is
run again.
The IRR is 11.13% for the example. The fact that it is greater
than 10%, the MARR means that the project is acceptable. The
IRR will always be greater than the MARR when the project net
present worth is positive. |
| |
|
The Cash Flow |
| |
|
For a complicated project with
several cash flow components, it is often difficult to determine
the flow of cash values in the several years of the project
life. For a tabular presentation choose Show Cash Flow from
the menu. In the resulting dialog, choose the project in the
name field. The buttons on the right select the results to
be displayed.
|
| |
|
| |
|
We have chosen to display the cash
flow in each period and the cumulative values. At the top of
the display is a series of measures that are computed with the
Excel economic functions. Row 17 indicates that this is a simple
investment, implying that the cumulative cash flow has only one
zero crossing. In this event the IRR is unique. The Payback is
the number of periods before the initial investment is recovered.
The MARR is an input value. Row 20 holds the minimum period index,
necessary for some of the computations. The NPW(0) is the net
present worth at time zero. The IRR guess is an input that will
effect the computed value of the IRR if that value is not unique.
Row 23 shows the computed value of the IRR. |
Graph of the Cash Flow |
| |
|
It is often instructive to view
a graph of the cash flow. Select Graph Cash Flow from
the menu and select the project name in the dialog. The terms Actual and Real refer
to different evaluations of the dollar amounts when inflation
is considered. With no inflation, we use Actual to
refer to the cash amounts at each period. The Cash Scale and
Time Scale control the size of the display.
A cash flow table must have already been constructed for a
project to appear on the name list. |
| |
|
| |
The cash flow for the
example is graphed below. Cash amounts at the same time are accumulated
to a single value. For example the 450 appearing at time 10 is
the sum of the salvage value of 400 and the net income of 50. |
| |
|
| |
We have illustrated
the evaluation of a single project when inflation and taxes
are neglected. The form holding the project data may be much
more complex than the simple example presented here. A project
may have several investments occurring at different times and
many annual receipts and disbursements. There is no limit to
the complexity the add-in can handle except the size of the
worksheet and the limitations of the user's computer.
The evaluation of projects with taxes and inflation is more
complex requiring additional data and more difficult computations.
The add-in handles these variations using commands and dialog
boxes similar to those illustrated on this page. |
| |
|





