|
|
|
|
Facility
Layout
|

|
-
Evaluation |
Problem |
| |
The layout problem is to arrange the physical spaces required
for several departments in a given space provided for the
departments. In practice the facility layout problem is often
solved by intuition, using the artistic and spatial skills
of the human designer; however, when there are quantitative
considerations associated with the layout problem, the human
is at a disadvantage as compared to the computer. In this
section we concentrate on computerized procedures for solving
the layout problem. In this section we explain the problem
by specifying the data and describing the decisions.
Here we are considering the problem of arranging several
departments on a plant with a single level and fixed rectangular
dimensions.
Certain data is necessary to describe the layout problem.
-
Number of departments, n,
-
Physical area of each department, 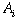
for i = 1… n
-
Physical dimensions of the plant in which
the departments are to be placed: Length, L, and
Width, W.
-
Product flow between every pair of departments:
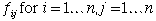
-
Material handling cost between every pair
of departments measured in dollars per unit-length measure:
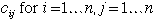
We illustrate the data requirement with an example used for
the Layout
add-in.
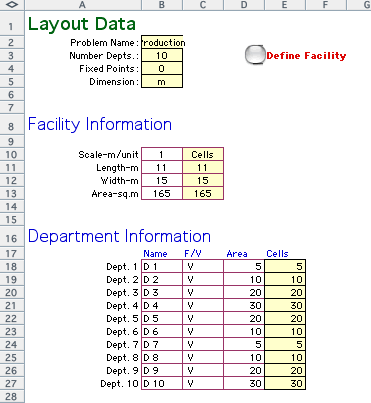
The example has 10 departments with various
area dimensions shown above. Area is specified in both a spatial
measure (square meters) and cells. For purposes of the add-in
the cell represents an indivisible area represented by a single
Excel worksheet cell. A scale factor is used to translate
between the spatial measure and the cell, for the example
it is one square meter to one cell. The F/V parameter indicates
whether the department is fixed or variable in location. For
the example all are variable.
The flow between departments is given in the
Flow Matrix. This chart is also called the From-To
matrix.
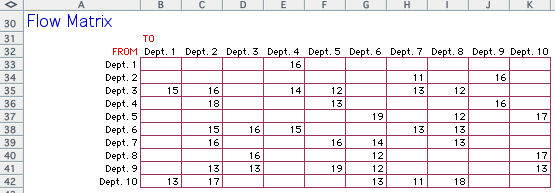
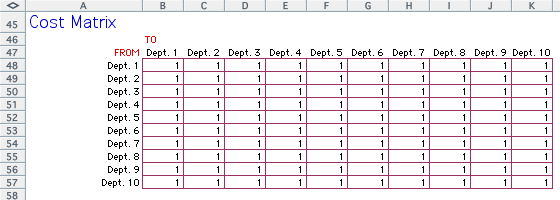
The material handling cost is 1 for all interdepartmental
flows for this example.
|
Distance |
| |
Our models involve the distance
from one department to another. The distance depends on the
layout. To illustrate consider a layout of the example departments
shown below. Since only the areas of the departments are specified
there are a great many possible layouts. We generally assume
that departments should not be split up into non-contiguous
areas and that they should be roughly rectangular shapes.
To construct the initial layout, the plant width is divided
into three equal width columns of 5 cells each. Starting in
the upper left corner the departments are placed in the plant
in numerical order passing down the first column. There is not
sufficient length to place the entire area of D4 in the first
column, so the remainder of D4 is placed in the second column.
The process continues going up in the second column until D8.
D9 and D10 are placed in the third column. Since the total area
of the departments is less than the area of the plant, some
cells remain unused at the bottom of the third column.

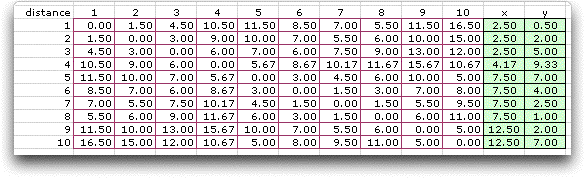
To develop a criterion for comparing layouts, distances are measured
between department centroids. We use the upper left corner of
the plant as the origin and compute the centroid (x,
y) as the distance below, y, and to the right,
x,of the origin. The centroids for the original layout
are in the two right-hand columns below.
There are different metrics one can use to evaluate
the distance between departments, including the Euclidean
distance and rectilinear distance measures. It is common
in layout analyses to use the rectilinear measure based on the
assumption that travel between departments will follow aisles
that are parallel to the borders of the facility.
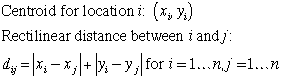
The distances between the departments for the
initial layout are given by the matrix above.
|
Criterion for Evaluation |
| |
We compute the cost for the flow from i
to j as the product of the material handling cost,
the flow, and the distance between the departments. The cost
of the layout is the sum of the flow costs.
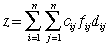
The cost for the initial layout is 4049.
The quantities 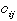 and and
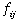 are
given as data, but the quantity are
given as data, but the quantity 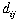 depends
on the layout. This makes optimization difficult. depends
on the layout. This makes optimization difficult. |
| |

|





