The second layout method considered is called the sequential method because every solution considered is described by a unique sequence of the first n integers. The search method moves from one sequence to another using a combinatorial search process.

The sequential method starts with an aisle layout and all subsequent solutions are also aisle layouts. We repeat the example with the initial solution determined with the sequence {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

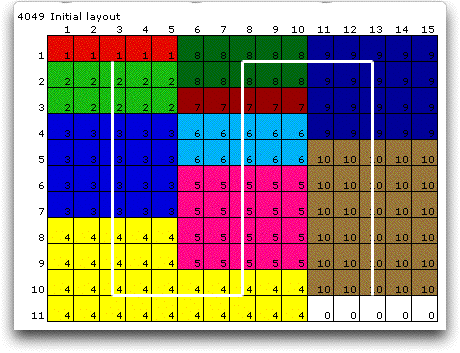
For this method all pairs of departments are considered for switching positions in the sequence. The layout is evaluated for every pair assuming that the positions in the sequence are switched. If a switch is discovered that results in a savings, the aisle layout based on the new sequence is constructed and used to continue the algorithm. For the example, the best switch is D9 and D10, resulting in the sequence {1, 2, 3, 4, 5, 6, 7, 8, 10, 9}. The resulting layout is shown below.

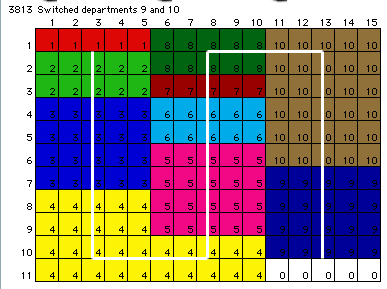
Since the construction of the layout given a sequence is well defined, this layout involves no arbitrary placement of departmental cells. When the initial layout has rectangular departments, the shapes of the departments remain rectangular except when a departments is placed in more than one aisle.

The next best switch is D1 and D3 resulting in the sequence {3, 2, 1, 4, 5, 6, 7, 8, 10, 9}. Notice that the change in sequence affects the relative locations of the departments switched. When the departments are of different size, the locations of all departments between are also adjusted. For the example, in addition to D1 and D3, the centroid of D2 is changed.

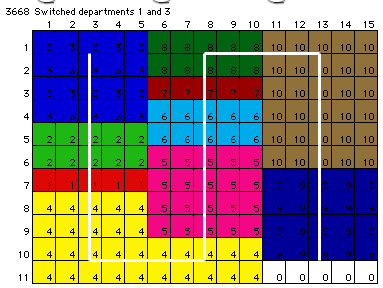
The process continues by switching D6 and D7 resulting in the sequence {3, 2, 1, 4, 5, 7, 6, 8, 10, 9}. The result is shown below.

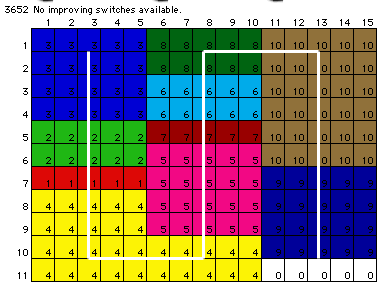
No improving switches are available after this step.

As for the CRAFT method, the final solution depends on the initial solution. There is no guarantee of optimality. The final solution is a local optimum when the neighborhood of adjacent solutions is the set of solutions reached by switching two departments in the sequence. The add-in can generate random initial solutions, so several local optimum may be generated, with the best selected as the layout to use.

Combinatorial Optimization

When the layout problem is stated as a problem of finding the optimum sequence, it can be addressed as a combinatorial optimization problem. We provide this capability through the Optimize command of the Layout add-in. This command requires that the Optimize add-in be installed. This add-in provides extensive search procedures for combinatorial permutation problems such as represented by the sequential layout problem. The add-in allows the user to specify the number of random starting solutions and the procedures used to improve the solutions. The solution below was determined by generating 10 random solutions and improving each with a two-change procedure.

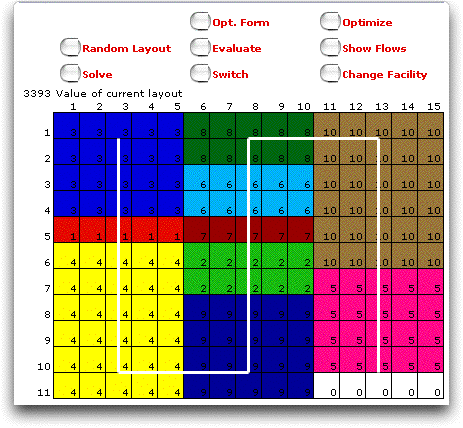
The solution method allows k-change variations of the sequence, where k can be any integer less than n - 1. Of course the larger values of k require many more computations than the 2-change solution illustrated. The Optimize add-in provides a list of the best solutions found during the search. The list for the example is below. A row shows the positions of the departments in the sequence. The figure above is the top entry in the list. D3 is the first in the sequence, D1 is the second and so on. The sequence represented by the top row is {3, 1, 4, 9, 2, 7, 6, 8, 10, 5}

The Layout add-in provides a variety of features that are described in the Computation section of this site. One is the graphical display of flows illustrated below.

The models may also specify that certain departments may be fixed in location or sequence. Fixed anchor points may be defined to represent features such as loading docks.