a. Show the network model that will find an optimum assignment of customers to service facilities. The goal is to minimize total shipping cost. Assume the total service capacity is greater than the total demand.

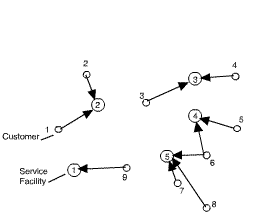
The figure below shows a schematic of the situation with one possible assignment of customers to service facilities. Note that it is possible to share the load from a particular customer as is illustrated for customer 6.

b. Add to the situation of the problem a cost of processing at the service stations. The unit cost of processing demand up to the amount m(j)/3 is p(j). The unit processing cost for amounts between m(j)/3 and 2m(j)/3 is 1.2 p(j). For any amount between 2m(j)/3 and m(j) the processing cost is 1.5p(j). m(j) and p(j)are parameters given for each service facility.

Now the goal is to minimize shipping plus processing costs. Show the change in the model necessary to accommodate this.

c. Consider the original problem situation (do not include the change in problem b). There is quite a bit of excess capacity in the system, so the company is changing a specified set of service facilities into collection points. Customers will ship to a collection point. The collection point will combine orders and then ship them to the service facilities. The return trip follows the same rout in reverse. Since shipments from collection points to service facilities will be in large volumes, total shipping cost may be reduced by this strategy.

Let e(i, j) be the roundtrip unit shipping cost from a collection point i to service facility j. When a service facility is a collection point it no longer will be able to to satisfy demand. If service facility j becomes a collection point its collection capacity is f(j).

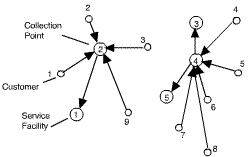
The figure shows a possible solution to the new situation in which facilities 2 and 4 have been turned into collection points. Facilities 1, 3 and 5 perform the service.

Show a network model to solve the new problem.