|
|
The picture below shows a traffic network. The arrows indicate
directions of allowed travel. Each arc has a travel time t(i,
j). These times are known, but are not shown on the network.
You have a minimum cost flow algorithm that has the parameters
(lower bound, upper bound, cost) for the arcs, and [fixed external
flow] for the nodes. Show the network models that will solve the
problems given below (one model for each part).
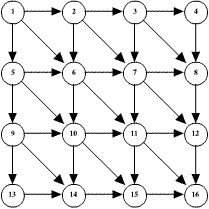
a. Find the shortest time route from node 1 to node 16
b. You want to send two vehicles from 1 to 16, but the two
must take entirely different paths. The two paths must not use
the same nodes or the same arcs. The total time for the two
vehicles is to be minimized.
c. Each arc has a capacity c(i, j), which is the number
of vehicles that can travel on that arc. In addition, every
node except node 16 has a supply of vehicles, where b(i)
is the number of vehicles at node i. Show the model that
would determine the maximum number of vehicles that could be
delivered to node 16 without exceeding the capacities on the
arcs or the vehicles available at the nodes.
d. As in part a, you want to direct a single vehicle through
the network from 1 to 16. The goal is to minimize total time
of travel. In addition, we have the constraint that the path
taken by the vehicle must use at least five arcs. Show the mathematical
programming model (objective function and constraints) that
will find this solution.
|



