|
|
 |
Decision
Analysis |
 |
-
Bayes' Analysis |
|
|
 |
Situations appropriate for decision analysis usually involve uncertainty.
Often tests are available to reduce the level of uncertainty.
Indeed part of the problem may be to decide whether or not to
perform the tests. Bayes' analysis helps to determine probabilities
for the branches of the decision tree.
|
| |
For the example problem,
there are five possible causes for the computer failure, labeled:
A, B, C, D and E. The first four are specific components of
the computer, while E represents all other causes. In the following,
we identify A through E as components. From past experience
the repair woman has probability estimates for each component.
These are called the prior probabilities.
P(A) = 0.15, P(B) =
0.,2, P(C) = 0.3,
P(D) = 0.25, P(E) =
0.1.
In terms of Bayes' analysis, A through E represent
the states of the world. The prior probabilities sum to 1,
because we require that all possible states have been enumerated.
We call the general prior probability P(y), where y is
one of the states.
The decision problem would be much easier if the repair woman
knew the state. Then the appropriate component would be replaced
and the expected cost of repair would be much reduced. The
repair woman can perform test X that will help identify the
failed component. The test has three possible outcomes: x1,
x2 and x3. Again through past experience she knows probabilities
of the three test outcomes when a specific component is failed.
These are called the conditional probabilities or the likelihood.
They are given in the table below. The notation P(x|y)
means the probability of outcome x given the state y.
P(x|y) |
A |
B |
C |
D |
E |
x1 |
0.6 |
0.7 |
0.15 |
0.05 |
0.1 |
x2 |
0.2 |
0.2 |
0.55 |
0.85 |
0.3 |
x3 |
0.2 |
0.1 |
0.3 |
0.1 |
0.6 |
These are not the probabilities necessary for decision analysis.
To construct the tree we need the probabilities that the test
will obtain each of the three outcomes, P(x).
These are called the Marginal Probabilities. We also
need the set of probabilities P(y|x),
that is, the probability of state y, given the experimental
outcome x. These are called the Posterior Probabilities.
Both sets of probabilities are readily available from the application
of Bayes' Rule, described in many introductory textbooks.
To construct the tables and do the computations for Bayes'
analysis, we select the Bayes' item from the OR_MM menu. The
dialog opens as below.

|
| |
For the example problem,
one of the five components has failed. A test, called Test1,
will help identify the failed component. In the general terms
of Bayes' analysis, we have five world states and three test
outcomes. We identify the states with the abbreviation Comp and
the test with the name Test.
The arrays that perform the Bayes' analysis can appear anywhere
on the worksheet with its upper left corner at the cell shown
at the field near the top of the dialog. The default cell is
where the cursor lies when the dialog is presented, but it
may be changed. Be sure that the arrays produced do not overwrite
cells that contain data or formulas. A default name is provided
when the dialog opens, but any legal Excel name may be used
(no spaces or punctuation, starting with a letter). We make
the practice of prefixing the name with the problem name so
that names are not duplicated on different sheets of the workbook.
The arrays can be placed on the worksheet with either the
states or outcomes on the horizontal as controlled by the buttons
at the bottom. It is traditional to show the states on the
horizontal, but when referencing the probabilities from worksheet
cells it may be more convenient to place the outcomes on the
horizontal. Both orientations are illustrated below. |
Analysis with States Horizontal |
| |
The figure shows the
section of the worksheet showing the Bayes' analysis. As usual,
yellow areas hold equations and should not be changed. All
computations are accomplished with standard Excel formulas.
The arrays with a white background and maroon borders are for
data entry. The likelihood values, P(x|y),
are entered in the cells starting at Z22. Note that it is not
necessary to enter the values in the row for x3. The columns
of the likelihood matrix must each sum to 1. We have assured
this result by placing an equation in the row for x3 that computes
1 less the sum of the other two rows.
The prior probabilities are entered in row 25 for the example.
It is unnecessary to provide an entry for E. It is computed
by a formula so that the sum or the prior probabilities is
equal to 1.
Of course, it is important that all probabilities entered
be non-negative and no greater than 1. |
| |
|
Marginal Probabilities |
| |
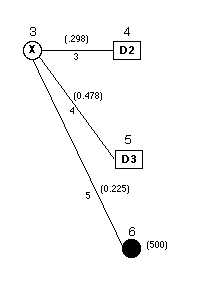 |
The marginal probabilities are computed
in column AE for the example. They are used in the decision
analysis for the probabilities on the arcs leaving node
3, the chance node representing the test X. |
|
| |
The figure below shows
the formulas that are placed on the worksheet for this model.
Rows 11, 12 and 13 of the worksheet model arcs 3, 4 and 5.
The formulas point to the marginal probabilities in column
AE of the Bayes' analysis. Note that we have used absolute
references ($) so that if the arc array is sorted the references
will not be disturbed.
The marginal probabilities could have also been referenced
using the Excel INDEX function. The formula for cell H11 would
be:
=INDEX(Repair_Test1_Marginal,1,1).
The marginal probabilities are given the name "Repair_Test1_Marginal"
on the worksheet. The INDEX function picks the entry from this
array in row 1 and column 1. The formula for cell H12 would
select the entry from the second row.
=INDEX(Repair_Test1_Marginal,2,1)
The INDEX function is very useful when using named arrays.
References are automatically absolute. Several other examples
appear below for arcs that use the posterior probabilities.
The name "Repair_Test1_Posterior" is assigned to
this array. |
| |
|
Analysis with Outcomes
Horizontal |
| |
The figure below shows
the test outcomes on the horizontal. The results are all the
same, but the numbers are transposed from the arrangement with
the states on the horizontal. |
| |
|
| |
Continued Testing |
| |
|
The example allows the repair
woman to perform two additional tests based on the result
of experiment X. From the posterior probabilities we note
that if test X has the outcome x1, the most likely source
of the failure is component A or B. Test Y is now available.
We assume that test Y can accurately identify the cause
of failure if it is due to component A or B. If either
of these indications are observed, the faulty component
is repaired. Every other cause (C, D, or E) is grouped
into a third category. If the test does not indicate A
or B, the motherboard is replaced. Since test Y is perfect,
the posterior probabilities for the failed component can
be taken directly from row x1 in the posterior probabilities
for test X. The results are shown on the figure at the
left.
Similarly when test X indicates x2, the cause is most
likely C or D. We can use test Z to accurately identify
the fault if it is due to C or D. If the test does not
indicate C or D, the fault must be in A, B or E. Rather
than continue testing, the motherboard is replaced. The
results of the tests together with the appropriate probabilities
are shown at the left. |
|
| |
|
|



