 |
An open queuing network can be optimized with the help of the
Optimize add-in.
The results of this page assume that the Optimize add-in
is installed as well as the Queuing add-in. We use
as an example the Job Shop network that was described earlier.
The model constructed by the Queuing add-in is shown below.
Our goal is to select the number of servers at each station
to satisfy constraints on results for the system. The numbers
of servers are the numbers in the range B5:G5. |
|
 |
To create an optimization model, we choose Optimize
Form from the Queue menu. We also show the Optimize
menu on the figure at the left because that add-in must
also be installed. We will deal directly with the Optimize
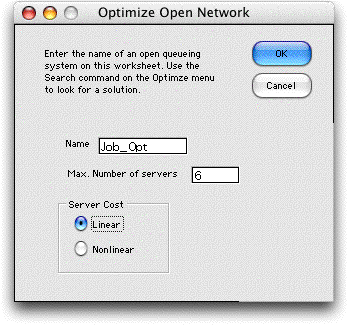
add-in through the Search command. The dialog
below is presented and we enter the name of the open
queuing system and a maximum for the number of servers.
A linear server cost indicates that each server in a
station has the same cost. A nonlinear server cost creates
a table so that different unit costs can be entered for
each station.
The Optimize add-in performs searches for discrete combinatorial
problems. It is applicable in many circumstances. The queuing
network provides an example of a search over the integers
to optimize a nonlinear objective function subject to nonlinear
constraints. |
|
| |
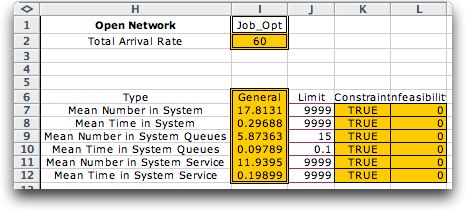
The Queuing add-in identifies cells
for constraints immediately to the right of the system results.
Column J holds the limit placed on the system result. Column
K holds formulas indicating whether the result is less than or
equal to the limit. Column L holds formulas computing the difference
between the result and the limit. For a feasible solution all
the cells in the range K7:K12 must be TRUE. The numbers shown
below are for the initial values of the variables. The constraints
are not satisfied for this solution. |
| |
|
| |
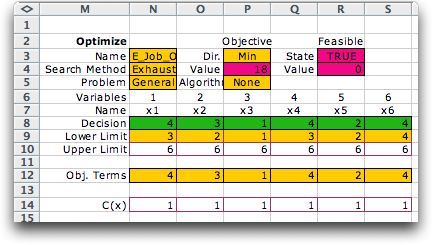
The Optimize add-in is automatically
called to construct a combinatorial optimization form starting
in column M. The cells colored green in row 8 hold the values
of the decision variables, the numbers of servers in each of
the six stations. Row 9 holds formulas that compute lower limits
to the numbers of servers. There must be at least the number
of servers at a station so that total service rate is greater
than the total arrival rate. The upper limits (6) were specified
in the dialog. These numbers may be changed after the form is
constructed. Row 14 holds the unit costs of the servers at the
stations. Since the example uses 1, we are minimizing the total
number of servers used. Row 12 computes the server cost for each
station. The sum of the yellow colored cells in row 12 is computed
in cell P4. This is the objective function for the model. Cell
R3 holds a logical expression that indicates whether all the
constraints are satisfied (they are not for the initial solution).
Cell R4 computes the amount of constraint violation. All formulas
in the yellow or pink cells are created by the add-ins and no
user interaction is required. |
| |
|
 |
One additional important step is accomplished
by the add-in. The numbers in the range N8:S8 are linked
to the queuing model by placing formulas in the cells B5:G5.
For example we see in cell B5 the formula:
=N8
The other cells are similarly linked. When the Optimize
add-in manipulates the numbers in N8:S8, the server numbers
in B5:G5 are changed. The functions in the queuing model
compute the system results in column J indicating whether
the solution is feasible. The variables are manipulated
by the Optimize add-in and the worksheet computes the
objective function and constraints.
To initiate optimization we choose Search from
the menu. The dialog that defines the search strategy
is shown below. There are many ways to search for the
optimum. For illustration we choose Exhaustive Enumeration.
This option will generate all values of the decision
variables within the lower and upper bounds and evaluate
the corresponding solutions. The add-in chooses the best
feasible solution. This option guarantees optimality,
but at the cost of many computations. |
|
| |
|
| |
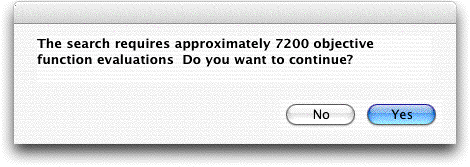
The add-in computes the number
of evaluations required and presents the number in a dialog
with the choice to continue or not.
After some time, the algorithm finally finishes
with the optimum solution shown below. The solution has 18
stations, which is the minimum number of stations that satisfies
the constraints. |
| |
The system results for the optimum solution fall
within the limits imposed. Individual station results are to
the left of this display starting in column A. The demonstration
file for this section has the complete worksheet.
To the right of the combinatorial form is a summary
of the time and number of runs required for the optimization.
There is always one extra run because the optimum solution
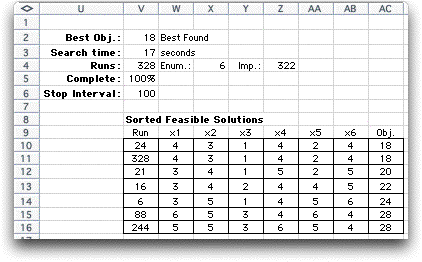
is repeated. The table below shows the 20 best solutions found.
There is only one solution with 18 servers that satisfies the
constraints, where there are several with 19 and 20.
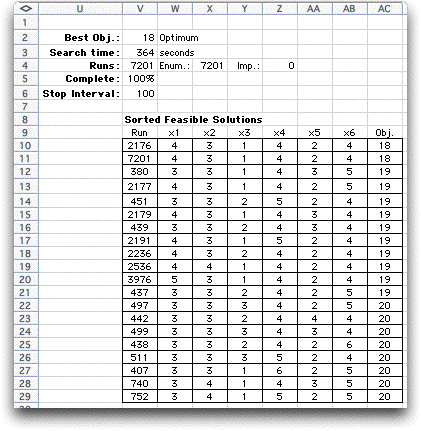
Although exhaustive enumeration finds the best
solution it takes a long time to find it. The approach is not
practical for larger numbers of variables or greater variable
ranges.
There are a number of heuristic alternatives
that do not guarantee the optimum, but often give good results.
The Greedy algorithm is a general procedure that changes
the variables one at a time. Starting from an initial solution,
the variable that improves the solution the most is increased
of decreased by 1, and the process repeats. The process terminates
when no change of a single variable improves the solution.
We choose Greedy with the Search dialog. |
| |
|
| |
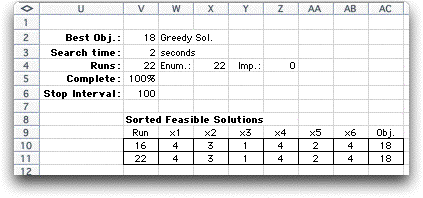
For the example, the Greedy algorithm
returned the optimum solution in 2 seconds on the author's
computer.
Another option is random search that may be followed
by an improvement process. The example below shows that 5 solutions
are to be generated randomly. Each random solution is to be
subjected to a 2-change procedure. The 2-change procedure selects
pairs of variables and attempts to increase and/or decrease
the variable values in an attempt to improve the solution.
All pairs are considered and the process continues until no
improvement is possible. |
| |
|
| |
The results are below. Again the
process finds the optimum. The runs are divided into Enumeration runs
and Improvement runs. The enumeration runs are the
five random solutions and the repeated optimum run. The improvement
runs are due the 2-change method.
|
| |
The Optimize add-in provides the
capability for finding the best values of the parameters of the
queuing system. Using the Optimize command of the Queue
menu builds the model described here. Optimization with different
objectives and constraints can be performed by using the Add
Form command on the Optimize menu. |
| |
|



