Computation - Operations Research Models and Methods

Computation

Queuing Add-in

Adding a Queue

Queuing Results

User Functions

Non-Markovian Queues

Non-Markovian User Functions

Open Networks

Job Shop Example

Non-Markovian Networks

Closed Networks

Queue Simulation

Optimize

Download

	Queuing Add-in
	- User Functions

The steady state results for Poisson Queuing systems are computed by user defined functions provided by the Queuing Add-in. These functions are in the Excel function list under the heading User Defined Functions. The function names all have the Q_ prefix. They are listed below with their parameters. The values are from the Q_Sample example. Most of the functions have a single argument which is the range defining the queue. The range is defined by the name given the queue. For example the first function would be Q_type(Q_Sample).

The range defined by a queue name holds five parameters: Lam = arrival rate when the system is empty, Mu = service rate for each server, ss = number of servers, SS_Max = maximum number in the system, PPop_Max = Size of the calling population. Leaving a blank for either of the latter two parameters or using non-numerical values implies that the parameter is infinity. For the Q_Sample example the parameters are in the range B2:B6 and take the values:

(5, 2, 3, ***, ***)

The *** used for the last two parameters indicate that the maximum number in the system and the population size are both infinite.

Function	Notation	Result
Q_type(Q_Sample): Determines the type of queue using Kendall's notation.	Type =	M/M/3
Q_L(Q_Sample): Computes the mean number in the system.	L=	6.011236
Q_W(Q_Sample): Computes the mean number in the system.	W =	1.2022472
Q_Lq(Q_Sample): Computes the mean number in the queue.	Lq=	3.511236
Q_Wq(Q_Sample): Computes the mean time in the queue.	Wq =	0.7022472
Q_Ls(Q_Sample): Computes the mean number in service.	Ls=	2.5
Q_Ws(Q_Sample): Computes the mean time in service.	Ws =	0.5
Q_LamB(Q_Sample): Computes the throughput of the station.	LamB =	5
Q_Eff(Q_Sample): Computes the efficiency of the servers.	Eff =	0.8333333
Q_P0(Q_Sample): Computes the probability of 0 in the system.	P0 =	0.0449438
Q_PB(Q_Sample): Computes the probability that all servers are busy.	PB =	0.7022472
Q_PF(Q_Sample): Computes the probability that the system is full.	PF =	0
Q_FNext(k, Q_Sample): The FNext function computes the factor to obtain the next probability in a series of state probabilities. The function must be multiplied by the previous probability. k is the index of the state computed. P(1) = P(0)*FNext(1, Queue)	P(1) =	0.1123596
Q_Pn(k, Q_Sample): Computes the probability of n customers in the system. Illustrated for 11.	P(11) =	0.02722
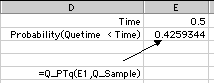
Q_PTq(time, Q_Sample):Computes the cumulative probability distribution of the waiting time in the queue. An example of this function is shown below.	PTq(0.5) =	0.4259344