Example: If you don’t win or lose on the first roll of the craps game, you might wonder how long the game will last. Assume the dice totals to 4 on the first roll. The player will continue to roll the dice until a 4 shows, and the player wins, or a 7 shows, and the player loses. Based on the probabilities computed earlier for a roll of a pair of dice, on any given roll, the game will end with probability 0.25 and continue with probability 0.75.

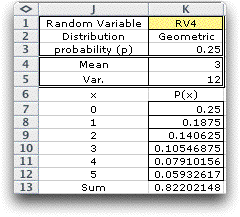
We define the random variable as the number of rolls prior to the last roll. That number may be 0, 1, 2,… which is random variable described by the geometric distribution. The results on the left show that the mean number of rolls is 3 and the variance is 12. The first six probabilities of the distribution are computed at the left. The game might continue for quite a few rolls. The probability that more than 5 rolls is required is about 0.18.